پرش به محتوا

هدایت الکتریکی

  • از
رسانایی اندازه گیری است سهولت عبور بار الکتریکی یا گرما از یک ماده. آ هادی ماده ای است که مقاومت بسیار کمی در برابر جریان می دهد جریان الکتریکی یا انرژی حرارتی مواد به عنوان فلز طبقه بندی می شوند، نیمه هادی ها و عایق ها فلزات رساناترین و عایق ترین هستند (سرامیک، چوب، پلاستیک) کمترین رسانایی را دارند.
رسانایی الکتریکی به ما می گوید که یک ماده چقدر به الکتریسیته اجازه می دهد از آن عبور کند. بسیاری از مردم سیم‌های مسی را چیزی می‌دانند که دارای برق عالی است هدایت تنظیم هدایت
هدایت حرارتی به ما می گوید که انرژی حرارتی (گرما برای اکثر اهداف) با چه راحتی می تواند انجام شود حرکت از طریق یک ماده برخی از مواد مانند فلزات اجازه عبور گرما را می دهند از طریق آنها به سرعت. تصور کنید که با یک دست شما در حال لمس کردن هستید یک تکه فلز و با دیگری یک تکه چوب. کدام مواد می تواند احساس سردی می کنی؟ اگر می گفتید “فلز” درست می گفتید. ولی، در واقع، هر دو ماده در واقع دمای یکسانی دارند. این نسبی است هدایت حرارتی. فلز قابلیت انتقال حرارت یا حرارت بالاتری دارد رسانایی، نسبت به چوب، اجازه می دهد گرمای دست شما سریعتر خارج شود. اگر شما می خواهید چیزی را سرد نگه دارید، بهترین ایده این است که آن را در چیزی بپیچید که قابلیت انتقال حرارت یا رسانایی حرارتی بالایی ندارد، این یک عایق خواهد بود سرامیک ها و پلیمرها معمولاً عایق های خوبی هستند. اما باید به خاطر داشته باشید که پلیمرها معمولا دمای ذوب بسیار پایینی دارند. این بدان معناست که اگر چیزی را طراحی می کنید که بسیار داغ شود، پلیمر بسته به دمای ذوب آن ممکن است ذوب شود.

هدایت الکتریکی و حرارتی هستند نزدیک مرتبط برای اکثر رساناهای الکتریکی خوب رسانای حرارتی خوبی نیز هستند.

بسیاری از محصولات حاوی هر دو هادی خواهند بود و عایق ها – هادی ها برق یا انرژی حرارتی را می گیرند جایی که می‌خواهد و عایق‌ها مانع از رسیدن آن به جایی می‌شوند مورد نظر نیست
عکس های نقره ای نقره بالاترین رسانایی الکتریکی را در بین تمام فلزات دارد. در واقع، نقره رسانایی را تعریف می کند – تمام فلزات دیگر با آن مقایسه می شوند آی تی. در مقیاس 0 تا 100، نقره رتبه 100، مس در 97 و طلا در 76. به دلیل این خاصیت، و به دلیل اینکه به راحتی جرقه نمی زند، نقره است معمولاً در مدارهای الکتریکی و کنتاکت ها استفاده می شود. نقره نیز مورد استفاده قرار می گیرد در باتری هایی که قابلیت اطمینان اجباری است و محدودیت وزن اعمال می شود، مانند ابزارهای جراحی قابل حمل، سمعک، ضربان ساز و سفر فضایی.

مقاومت و رسانایی الکتریکی

از ویکیپدیا، دانشنامه آزاد
(تغییر مسیر از رسانایی الکتریکی )

پرش به پیمایش پرش به جستجو

این مقاله به طور کلی در مورد هدایت الکتریکی است. برای سایر انواع رسانایی، رسانایی . برای کاربردهای خاص در عناصر الکتریکی، مقاومت و رسانایی الکتریکی .
مقاومت
نمادهای رایج
 ρ
واحد SI اهم متر (Ω⋅m)
در واحدهای پایه SI kg⋅m 3 ⋅s −3 ⋅A −2
مشتقات از
مقادیر دیگر
 ρ = آر آ ℓ {\ displaystyle \ rho = R {\ frac {A} {\ ell}}}
بعد، ابعاد، اندازه م L 3 تی – 3 من – 2 {\displaystyle {\mathsf {M}}{\mathsf {L}}^{3}{\mathsf {T}}^{-3}{\mathsf {I}}^{-2}}
رسانایی
نمادهای رایج
 σ، κ، γ
واحد SI زیمنس بر متر (S/m)
در واحدهای پایه SI kg −1 ⋅m −3 ⋅s 3 ⋅A 2
مشتقات از
مقادیر دیگر
 σ = 1 ρ {\displaystyle \sigma ={\frac {1}{\rho }}}
بعد، ابعاد، اندازه م – 1 L – 3 تی 3 من 2 {\displaystyle {\mathsf {M}}^{-1}{\mathsf {L}}^{-3}{\mathsf {T}}^{3}{\mathsf {I}}^{2}}

مقاومت الکتریکی نیز نامیده می شود مقاومت الکتریکی خاص یا حجمی ) یک ویژگی اساسی یک ماده است که میزان مقاومت آن در برابر جریان الکتریکی گیرد. مقاومت پایین ماده ای را نشان می دهد که به راحتی جریان الکتریکی را می دهد. مقاومت معمولاً با حرف یونانی ρ ( rho ) نشان داده می شود. واحد SI مقاومت الکتریکی اهم ( متر Ω⋅m) است. [1] [2] [3] به عنوان مثال، اگر یک متر 1 مکعبی از مواد دارای تماس های صفحه ای در دو وجه متضاد باشد و مقاومت بین این کنتاکت ها 1 Ω باشد، پس مقاومت ماده 1 Ω⋅m باشد. .

رسانایی الکتریکی یا رسانایی خاص ، متقابل مقاومت الکتریکی است. این نشان دهنده توانایی یک ماده برای هدایت جریان الکتریکی است. معمولاً با حرف یونانی σ ( سیگما ) نشان داده می شود، اما κ ( کاپا ) (به ویژه در مهندسی برق) و γ ( گاما ) گاهی اوقات استفاده می شود. واحد SI هدایت الکتریکی زیمنس بر متر (S/m) است.

تعریف

مورد ایده آل

قطعه ای از مواد مقاوم با تماس های الکتریکی در دو انتها.

در حالت ایده آل، سطح مقطع و ترکیب فیزیکی مواد مورد بررسی در سراسر نمونه یکنواخت است و میدان الکتریکی و چگالی جریان در همه جا موازی و ثابت هستند. بسیاری از مقاومت ها و هادی ها در واقع دارای سطح مقطع یکنواخت با جریان الکتریکی یکنواخت هستند و از یک ماده واحد ساخته شده اند، بنابراین این مدل خوبی است. (نمودار مجاور را ببینید.) هنگامی که این مورد است، مقاومت الکتریکی ρ (به یونانی: rho ) را می توان به صورت زیر محاسبه کرد:

 

ρ = آر آ ℓ ، {\ displaystyle \ rho = R {\ frac {A} {\ ell}},}

 

جایی که

  • آر {\displaystyle R} مقاومت الکتریکی یک نمونه یکنواخت از ماده است
  • ℓ {\displaystyle \ell } است طول نمونه
  • آ {\displaystyle A} سطح مقطع نمونه است

مقاومت را می توان با استفاده از SI واحد اهم  متر (Ω⋅m) بیان کرد – یعنی اهم ضرب در متر مربع (برای سطح مقطع) سپس تقسیم بر متر (برای طول).

هم مقاومت و مقاومت توضیح می دهند که عبور جریان الکتریکی از یک ماده چقدر دشوار است، اما بر خلاف مقاومت، مقاومت یک ویژگی ذاتی است . این بدان معناست که تمام سیم‌های مسی خالص (که در معرض اعوجاج ساختار کریستالی و غیره قرار نگرفته‌اند)، صرف نظر از شکل و اندازه‌شان، مقاومت ، اما یک سیم مسی بلند و نازک مقاومت نسبت به سیم‌های ضخیم دارد. ، سیم مسی کوتاه. هر ماده ای مقاومت ویژه خود را دارد. به عنوان مثال، لاستیک مقاومت بسیار بیشتری نسبت به مس دارد.

در یک قیاس هیدرولیکی ، عبور جریان از یک ماده با مقاومت بالا مانند فشار دادن آب از طریق یک لوله پر از شن است – در حالی که عبور جریان از یک ماده با مقاومت کم مانند فشار دادن آب از طریق یک لوله خالی است. اگر لوله ها هم اندازه و هم شکل باشند، لوله پر از ماسه مقاومت بیشتری در برابر جریان دارد. با این حال، مقاومت تنها با وجود یا عدم وجود ماسه تعیین نمی شود. این به طول و عرض لوله نیز بستگی دارد: لوله های کوتاه یا پهن مقاومت کمتری نسبت به لوله های باریک یا بلند دارند.

معادله فوق را می توان برای بدست آوردن قانون پویه (به نام کلود پویه ) جابه جا کرد:

 

آر = ρ ℓ آ . {\ displaystyle R = \ rho {\ frac {\ ell} {A}}.}

مقاومت یک عنصر معین با طول متناسب است، اما با سطح مقطع نسبت معکوس دارد. به عنوان مثال، اگر A = 1 متر مربع ، ℓ {\displaystyle \ell } = 1 متر (تشکیل یک مکعب با تماس های کاملا رسانا در وجوه مخالف)، سپس مقاومت این عنصر بر حسب اهم از نظر عددی برابر با مقاومت ماده ای است که از آن ساخته شده است در Ω⋅m.

 

رسانایی، σ ، معکوس مقاومت است:

 

σ = 1 ρ . {\displaystyle \sigma ={\frac {1}{\rho }}.}

 

رسانایی دارای واحدهای SI زیمنس بر متر (S/m) است.

کمیت های اسکالر عمومی سنسور هدایت الکتریکی

برای موارد کمتر ایده آل، مانند هندسه پیچیده تر، یا زمانی که جریان و میدان الکتریکی در قسمت های مختلف ماده متفاوت است، لازم است از یک عبارت کلی تر استفاده شود که در آن مقاومت در یک نقطه خاص به عنوان نسبت میدان الکتریکی به چگالی جریانی که در آن نقطه ایجاد می کند:

 

ρ = E جی ، {\displaystyle \rho ={\frac {E}{J}},}

 

جایی که

  • ρ {\displaystyle \rho } مقاومت ماده هادی است،
  • E {\displaystyle E} میدان قدر الکتریکی است،
  • جی {\displaystyle J} مقدار چگالی جریان است،

که در آن E {\displaystyle E} و جی {\displaystyle J} داخل هادی هستند.

رسانایی معکوس (متقابل) مقاومت است. در اینجا، توسط:

 

σ = 1 ρ = جی E . {\displaystyle \sigma ={\frac {1}{\rho }}={\frac {J}{E}}.}

 

به عنوان مثال، لاستیک ماده ای با ρ کوچک σ – زیرا حتی یک میدان الکتریکی بسیار بزرگ در لاستیک تقریباً هیچ جریانی از آن عبور نمی کند. از سوی دیگر، مس ماده ای با ρ بزرگ σ – زیرا حتی یک میدان الکتریکی کوچک جریان زیادی را از آن عبور می دهد.

همانطور که در زیر نشان داده شده است، این عبارت زمانی که میدان الکتریکی و چگالی جریان در ماده ثابت باشد به یک عدد ساده می‌شود.
اشتقاق از تعریف کلی مقاومت

مقاومت تانسور

هنگامی که مقاومت یک ماده دارای یک جزء جهت است، باید از کلی ترین تعریف مقاومت استفاده شود. این قانون از شکل تانسور-بردار قانون اهم که میدان الکتریکی درون یک ماده را به جریان جریان الکتریکی مرتبط می کند. این معادله کاملاً کلی است یعنی در همه موارد از جمله موارد ذکر شده در بالا معتبر است. با این حال، این تعریف پیچیده ترین است، بنابراین فقط به طور مستقیم در ناهمسانگرد ، جایی که تعاریف ساده تر را نمی توان اعمال کرد. اگر ماده ناهمسانگرد نباشد، می توان از تعریف تانسور-بردار چشم پوشی کرد و به جای آن از یک عبارت ساده تر استفاده کرد.

در اینجا ناهمسانگرد به این معنی است که ماده دارای خواص متفاوتی در جهات مختلف است. به عنوان مثال، یک کریستال گرافیت از نظر میکروسکوپی از یک پشته ورقه تشکیل شده است و جریان به راحتی از هر ورقه عبور می کند، اما به راحتی از یک ورق به ورق مجاور آن بسیار کمتر است. [4] در چنین مواردی، جریان دقیقاً در جهت میدان الکتریکی جریان ندارد. بنابراین، معادلات مناسب به شکل تانسور سه بعدی تعمیم داده می شوند: [5] [6]

 

که در آن رسانایی σ و مقاومت ρ رتبه-2 تانسورهای هستند و میدان الکتریکی E و چگالی جریان J بردار هستند. این تانسورها را می توان با ماتریس های 3×3، بردارها با ماتریس های 3×1، با ضرب ماتریس در سمت راست این معادلات نشان داد. در شکل ماتریسی، رابطه مقاومت به صورت زیر بدست می آید:

جایی که

  • E {\displaystyle \mathbf {E} } بردار میدان الکتریکی با اجزای Ex Ey , Ez ( , ) است .
  • ρ {\ displaystyle {\ boldsymbol {\ rho}}} تانسور مقاومت، به طور کلی یک ماتریس سه در سه است.
  • جی {\displaystyle \mathbf {J} } بردار چگالی جریان الکتریکی با اجزای ( J x ، J y ، J z ) است.

به طور معادل، مقاومت را می توان در نماد فشرده تر اینشتین :

 

E من = ρ من j جی j   . {\ displaystyle \ mathbf {E} _ {i} = {\ boldsymbol {\ rho}} _ {ij} \ mathbf {J} _ {j} ~.}

در هر صورت، عبارت حاصل برای هر جزء میدان الکتریکی به صورت زیر است:

E ایکس = ρ ایکس ایکس جی ایکس + ρ ایکس Y جی Y + ρ ایکس z جی z E Y = ρ Y ایکس جی ایکس + ρ Y Y جی Y + ρ Y z جی z E z = ρ z ایکس جی ایکس + ρ z Y جی Y + ρ z z جی z {\displaystyle {\begin{aligned}E_{x}&=\rho _{xx}J_{x}+\rho _{xy}J_{y}+\rho _{xz}J_{z}\\E_ {y}&=\rho _{yx}J_{x}+\rho _{yy}J_{y}+\rho _{yz}J_{z}\\E_{z}&=\rho _{zx }J_{x}+\rho _{zy}J_{y}+\rho _{zz}J_{z}\end{تراز شده}}}

از آنجایی که انتخاب سیستم مختصات آزاد است، قرارداد معمول این است که عبارت را با انتخاب یک x موازی با جهت فعلی ساده کنیم، بنابراین J y = J z = 0 . این باعث می شود:

ρ ایکس ایکس = E ایکس جی ایکس ، ρ Y ایکس = E Y جی ایکس ، و ρ z ایکس = E z جی ایکس . {\displaystyle \rho _{xx}={\frac {E_{x}}{J_{x}}},\quad \rho _{yx}={\frac {E_{y}}{J_{x} }}،{\text{ و }}\rho _{zx}={\frac {E_{z}}{J_{x}}}.}

رسانایی به طور مشابه تعریف شده است: [7]

یا

هر دو منجر به:

جی ایکس = σ ایکس ایکس E ایکس + σ ایکس Y E Y + σ ایکس z E z جی Y = σ Y ایکس E ایکس + σ Y Y E Y + σ Y z E z جی z = σ z ایکس E ایکس + σ z Y E Y + σ z z E z {\displaystyle {\begin{aligned}J_{x}=\sigma _{xx}E_{x}+\sigma _{xy}E_{y}+\sigma _{xz}E_{z}\\J_{ y}=\sigma _{yx}E_{x}+\sigma _{yy}E_{y}+\sigma _{yz}E_{z}\\J_{z}=\sigma _{zx}E_{ x}+\sigma _{zy}E_{y}+\sigma _{zz}E_{z}\end{تراز شده}}}

 

با نگاهی به این دو عبارت،. ماتریس معکوس یکدیگر هستند با این حال، در کلی‌ترین حالت، عناصر ماتریس مجزا لزوماً متقابل یکدیگر نیستند. برای مثال، σ xx ممکن است برابر با 1/ ρ xx . این را می توان در جلوه هال ، جایی که ρ ایکس Y {\displaystyle \rho _{xy}} غیر صفر است در اثر هال، به دلیل تغییر ناپذیری چرخشی حول z ، ρ Y Y = ρ ایکس ایکس {\displaystyle \rho _{yy}=\rho _{xx}} و ρ Y ایکس = – ρ ایکس Y {\displaystyle \rho _{yx}=-\rho _{xy}} بنابراین رابطه بین مقاومت و رسانایی ساده می شود: [8]

اگر میدان الکتریکی با جریان اعمال شده موازی باشد، ρ ایکس Y {\displaystyle \rho _{xy}} و ρ ایکس z {\displaystyle \rho _{xz}} صفر هستند. وقتی صفر هستند، یک عدد، ρ ایکس ایکس {\displaystyle \rho _{xx}} ، برای توصیف مقاومت الکتریکی کافی است. سپس به صورت ساده نوشته می شود ρ {\displaystyle \rho } ، و این به عبارت ساده تر کاهش می یابد.

رسانایی و حامل های جریان

رابطه بین چگالی جریان و سرعت جریان الکتریکی

جریان الکتریکی حرکت مرتب بارهای الکتریکی است. این هزینه ها را حامل های جاری می نامند. در فلزات و نیمه هادی ها ، الکترون ها حامل جریان هستند. در الکترولیت ها و گازهای یونیزه ، یون های مثبت و منفی . در حالت کلی، چگالی جریان یک حامل با فرمول تعیین می شود: [9]

j → = q n υ → آ   ، {\ displaystyle {\ vec {j}} = qn {\ vec {\ upsilon}} _ {a} ~,}

که در آن n چگالی حامل های بار (تعداد حامل ها در یک واحد حجم)، q بار یک حامل، و υ → آ {\ displaystyle {\ vec {\ upsilon}} _ {a}} میانگین سرعت حرکت آنها است. در موردی که جریان از حامل های زیادی تشکیل شده باشد

j → = ∑ j j من   . {\displaystyle {\vec {j}}=\sum _{j}j_{i}~.}

 

جایی که j من {\displaystyle j_{i}} چگالی جریان است من {\displaystyle i} حامل -ام.

علل رسانایی

نظریه باند ساده شده

همچنین نگاه کنید به: نظریه باند

پر کردن حالات الکترونیکی در انواع مختلف مواد در حالت تعادل . در اینجا، ارتفاع انرژی است در حالی که عرض چگالی حالات موجود برای انرژی خاصی در مواد ذکر شده است. سایه از توزیع فرمی دیراک ( سیاه : همه حالات پر شده، سفید : هیچ حالتی پر نشده است). در فلزات و نیمه سطح فرمی E F حداقل در داخل یک نوار قرار دارد.

در عایق ها و نیمه هادی ها سطح فرمی در داخل یک شکاف نواری قرار دارد. با این حال، در نیمه رساناها، نوارها به اندازه کافی به سطح فرمی نزدیک هستند تا از نظر حرارتی با الکترون ها یا سوراخ ها شوند.

ویرایش کنید

طبق مکانیک کوانتومی ، یک الکترون در یک اتم یا کریستال فقط می‌تواند سطوح انرژی دقیق خاصی داشته باشد. انرژی بین این سطوح غیرممکن است. هنگامی که تعداد زیادی از چنین سطوح مجاز دارای مقادیر انرژی نزدیک به هم هستند – یعنی انرژی هایی دارند که فقط به طور جزئی با هم تفاوت دارند – این سطوح انرژی نزدیک در ترکیب “باند انرژی” نامیده می شود. بسته به عدد اتمی اتم‌های تشکیل‌دهنده [a] و توزیع آن‌ها در کریستال، می‌تواند تعداد زیادی از این باندهای انرژی در یک ماده وجود داشته باشد. [ب]

الکترون‌های این ماده با ته‌نشین شدن در حالت‌های کم انرژی به دنبال به حداقل رساندن انرژی کل در ماده هستند. با این حال، اصل طرد پاولی به این معنی است که در هر یک از این حالت ها فقط یک می تواند وجود داشته باشد. بنابراین الکترون‌ها ساختار نواری را که از پایین شروع می‌شود، پر می‌کنند. سطح انرژی مشخصه ای که الکترون ها تا آن اندازه پر شده اند، تراز فرمی . موقعیت تراز فرمی با توجه به ساختار نواری برای هدایت الکتریکی بسیار مهم است: فقط الکترون‌هایی که در سطوح انرژی نزدیک یا بالاتر از سطح فرمی قرار دارند، آزاد هستند تا در ساختار مواد گسترده‌تر حرکت کنند، زیرا الکترون‌ها می‌توانند به راحتی در میان مواد نیمه اشغال شده بپرند. ایالت های آن منطقه در مقابل، حالت‌های کم انرژی به طور کامل با یک محدودیت ثابت در تعداد الکترون‌ها در همه زمان‌ها پر می‌شوند و حالت‌های انرژی بالا همیشه خالی از الکترون هستند.

جریان الکتریکی از جریانی از الکترون ها تشکیل شده است. در فلزات سطوح انرژی الکترون های زیادی در نزدیکی سطح فرمی وجود دارد، بنابراین الکترون های زیادی برای حرکت در دسترس هستند. این همان چیزی است که باعث هدایت الکترونیکی بالای فلزات می شود.

بخش مهمی از نظریه باند این است که ممکن است باندهای ممنوعه انرژی وجود داشته باشد: فواصل انرژی که هیچ سطح انرژی ندارند. در عایق ها و نیمه هادی ها، تعداد الکترون ها دقیقاً به اندازه ای است که تعداد صحیح مشخصی از باندهای کم انرژی را دقیقاً تا مرز پر می کند. در این مورد، سطح فرمی در یک شکاف باند قرار می گیرد. از آنجایی که هیچ حالتی در نزدیکی سطح فرمی وجود ندارد، و الکترون ها آزادانه حرکت نمی کنند، رسانایی الکترونیکی بسیار پایین است.

در فلزات

مقاله اصلی: مدل الکترون آزاد
مانند توپ‌هایی که در گهواره نیوتن هستند ، الکترون‌های یک فلز به سرعت انرژی را از یک پایانه به پایانه دیگر منتقل می‌کنند، علی‌رغم حرکت ناچیز خود.

یک فلز از شبکه ای از اتم ها که هر کدام دارای یک پوسته بیرونی از الکترون ها هستند که آزادانه از اتم های اصلی خود جدا شده و از طریق شبکه عبور می کنند. این همچنین به عنوان یک شبکه یونی مثبت شناخته می شود. [10] این “دریای” الکترونهای قابل تفکیک به فلز اجازه می دهد تا جریان الکتریکی را هدایت کند. هنگامی که یک اختلاف پتانسیل الکتریکی ( ولتاژ ) روی فلز اعمال می شود، میدان الکتریکی حاصل باعث می شود که الکترون ها به سمت ترمینال مثبت حرکت کنند. واقعی سرعت رانش الکترون‌ها معمولاً کوچک است، در مرتبه بزرگی متر در ساعت. با این حال، به دلیل تعداد زیاد الکترون های متحرک، حتی یک سرعت رانش آهسته منجر به چگالی جریان می شود. [11] این مکانیسم شبیه به انتقال تکانه توپ ها در گهواره نیوتن است [12] اما انتشار سریع انرژی الکتریکی در طول یک سیم به دلیل نیروهای مکانیکی نیست، بلکه انتشار یک میدان الکترومغناطیسی حامل انرژی است که هدایت می شود. توسط سیم

اکثر فلزات دارای مقاومت الکتریکی هستند. در مدل‌های ساده‌تر (مدل‌های مکانیکی غیر کوانتومی) این را می‌توان با جایگزینی الکترون‌ها و شبکه کریستالی با ساختاری موج‌مانند توضیح داد. هنگامی که موج الکترونی از شبکه عبور می کند، امواج تداخل که باعث مقاومت می شود. هرچه شبکه منظم تر باشد، اختلال کمتری ایجاد می کند و در نتیجه مقاومت کمتری دارد. بنابراین مقدار مقاومت عمدتاً توسط دو عامل ایجاد می شود. اولاً ناشی از دما و در نتیجه مقدار ارتعاش شبکه کریستالی است. دمای بالاتر باعث ایجاد ارتعاشات بزرگتر می شود که به عنوان بی نظمی در شبکه عمل می کند. دوم، خلوص فلز مرتبط است زیرا مخلوطی از یون‌های مختلف نیز یک بی‌نظمی است. [13] [14] کاهش اندک در رسانایی در ذوب فلزات خالص به دلیل از بین رفتن نظم بلوری دوربرد است. ترتیب برد کوتاه باقی می ماند و همبستگی قوی بین موقعیت های یون ها منجر به انسجام بین امواج پراش شده توسط یون های مجاور می شود. [15]

در نیمه هادی ها و عایق ها

مقالات اصلی: نیمه هادی و عایق (برق)

در فلزات، سطح فرمی در نوار رسانایی (به نظریه باند، در بالا مراجعه کنید) که باعث ایجاد الکترون های هدایت آزاد می شود. با این حال، در نیمه رساناها ، موقعیت تراز فرمی در داخل شکاف نواری است، تقریباً در نیمه راه بین حداقل نوار رسانایی (پایین اولین باند سطوح انرژی الکترون پر نشده) و حداکثر باند ظرفیت (بالای نوار زیر رسانش). باند، سطوح انرژی الکترون پر شده). این در مورد نیمه هادی های ذاتی (بدون دوش) صدق می کند. این بدان معنی است که در دمای صفر مطلق، هیچ الکترون رسانایی آزاد وجود نخواهد داشت و مقاومت بی نهایت است. با این حال، با افزایش چگالی حامل بار (یعنی بدون ایجاد عوارض بیشتر، چگالی الکترون ها) در نوار رسانایی، مقاومت کاهش می یابد. در نیمه هادی های بیرونی (دوپ شده)، ناخالص با اهدای الکترون به نوار رسانایی یا ایجاد حفره هایی در نوار ظرفیت، غلظت حامل بار اصلی را افزایش می دهند. («حفره» موقعیتی است که در آن یک الکترون وجود ندارد؛ چنین حفره‌هایی می‌توانند رفتاری مشابه الکترون‌ها داشته باشند.) برای هر دو نوع اتم دهنده یا گیرنده، افزایش چگالی ناخالص مقاومت را کاهش می‌دهد. از این رو، نیمه هادی های بسیار دوپ شده رفتار فلزی دارند. در دماهای بسیار بالا، سهم حامل های حرارتی تولید شده بر سهم اتم های ناخالص غالب است و مقاومت به طور تصاعدی با دما کاهش می یابد.

در مایعات یونی/الکترولیت

نوشتار اصلی: رسانایی (الکترولیتی)

در الکترولیت‌ها ، رسانش الکتریکی توسط الکترون‌ها یا حفره‌های نواری اتفاق نمی‌افتد، بلکه توسط گونه‌های اتمی کامل ( یون‌ها ) که در حال حرکت هستند و هر یک حامل بار الکتریکی هستند، اتفاق می‌افتد. مقاومت محلول های یونی (الکترولیت ها) با غلظت بسیار متفاوت است – در حالی که آب مقطر تقریباً یک عایق است، آب نمک یک رسانای الکتریکی معقول است. رسانایی در مایعات یونی نیز با حرکت یون ها کنترل می شود، اما در اینجا ما در مورد نمک های مذاب صحبت می کنیم تا یون های حل شده. در غشاهای بیولوژیکی ، جریان ها توسط نمک های یونی حمل می شوند. سوراخ‌های کوچک در غشای سلولی که کانال‌های یونی می‌شوند نسبت به یون‌های خاص انتخابی هستند و مقاومت غشا را تعیین می‌کنند.

غلظت یون ها در یک مایع ( مثلاً در یک محلول آبی) به درجه تفکیک ماده محلول بستگی دارد که با ضریب تفکیک مشخص می شود. آ {\displaystyle \alpha } ، که نسبت غلظت یون ها است ن {\displaystyle N} به غلظت مولکول های ماده محلول ن 0 {\displaystyle N_{0}} :

 

ن = آ ن 0   . {\displaystyle N=\alpha N_{0}~.}

 

هدایت الکتریکی خاص ( σ {\displaystyle \sigma } ) یک راه حل برابر است با:

 

σ = q ( ب + + ب – ) آ ن 0   ، {\\sigma =q\left(b^{+}+b^{-}\right)\N_{0}~,}

 

جایی که q {\displaystyle q} : ماژول شارژ یونی، ب + {\b^{+}} و ب – {\b^{-}} : تحرک یون های دارای بار مثبت و منفی، ن 0 {\N_{0}} : غلظت مولکول های ماده محلول، آ {\displaystyle \alpha } : ضریب تفکیک.

ابررسانایی

مقاله اصلی: ابررسانایی

داده های اصلی از آزمایش 1911 توسط هایک کامرلینگ اونس که مقاومت یک سیم جیوه ای را به عنوان تابعی از دما نشان می دهد. افت ناگهانی مقاومت، انتقال ابررسانا است.

مقاومت الکتریکی یک رسانای فلزی به تدریج با کاهش دما کاهش می یابد. در هادی های معمولی (یعنی غیر ابررسانا) مانند مس یا نقره ، این کاهش توسط ناخالصی ها و سایر عیوب محدود می شود. حتی نزدیک به صفر مطلق ، یک نمونه واقعی از یک هادی معمولی مقداری مقاومت نشان می دهد. در یک ابررسانا، هنگامی که ماده زیر دمای بحرانی خود خنک می شود، مقاومت به طور ناگهانی به صفر می رسد. در یک هادی معمولی، جریان توسط یک گرادیان ولتاژ هدایت می‌شود، در حالی که در یک ابررسانا، شیب ولتاژی وجود ندارد و جریان به شیب فاز پارامتر مرتبه ابررسانا مربوط می‌شود. [16] پیامد این امر این است که یک جریان الکتریکی که در حلقه ای از سیم ابررسانا می تواند به طور نامحدود بدون منبع انرژی باقی بماند.

در دسته ای از ابررساناها

که به عنوان ابررساناهای نوع II ، از جمله همه ابررساناهای شناخته شده با دمای بالا ، یک مقاومت بسیار کم اما غیر صفر در دماهایی که خیلی کمتر از انتقال ابررسانا اسمی نیستند، زمانی که یک جریان الکتریکی همراه با یک میدان مغناطیسی قوی اعمال می شود، ظاهر می شود. که ممکن است ناشی از جریان الکتریکی باشد. این به دلیل حرکت گردابه های مغناطیسی در ابرسیال الکترونیکی است که مقداری از انرژی حمل شده توسط جریان را از بین می برد. مقاومت ناشی از این اثر در مقایسه با مقاومت مواد غیر ابررسانا ناچیز است، اما باید در آزمایش‌های حساس مورد توجه قرار گیرد. با این حال، با کاهش دما به اندازه کافی کمتر از انتقال اسمی ابررسانا، این گرداب ها می توانند منجمد شوند به طوری که مقاومت ماده واقعاً صفر شود.

پلاسما

مقاله اصلی: پلاسما (فیزیک)

رعد و برق نمونه ای از پلاسمای موجود در سطح زمین است. به طور معمول، رعد و برق 30000 آمپر را تا 100 میلیون ولت تخلیه می کند و نور، امواج رادیویی و اشعه ایکس ساطع می کند. [18] دمای پلاسما در رعد و برق ممکن است به 30000 کلوین (29727 درجه سانتیگراد) (53540 درجه فارنهایت) یا پنج برابر گرمتر از دمای سطح خورشید نزدیک شود و چگالی الکترونها ممکن است از 1024 m – 3 .

پلاسما هادی های بسیار خوبی هستند و پتانسیل های الکتریکی نقش مهمی دارند.

پتانسیلی که به طور متوسط ​​در فضای بین ذرات باردار وجود دارد، مستقل از این که چگونه می توان آن را اندازه گیری کرد، پتانسیل پلاسما یا پتانسیل فضایی . اگر یک الکترود در پلاسما قرار داده شود، پتانسیل آن معمولاً به میزان قابل توجهی زیر پتانسیل پلاسما قرار می گیرد، زیرا به آن غلاف Debye می . رسانایی الکتریکی خوب پلاسماها میدان الکتریکی آنها را بسیار کوچک می کند. این منجر به مفهوم مهم ne ، که می گوید چگالی بارهای منفی تقریباً برابر با چگالی بارهای مثبت در حجم زیاد پلاسما است ( n ⟨Z⟩ > شود i )، اما در مقیاس Debye طول می تواند عدم تعادل شارژ وجود داشته باشد. در حالت خاصی که لایه‌های دوتایی تشکیل می‌شوند، جداسازی شارژ می‌تواند ده‌ها طول Debye را افزایش دهد.

بزرگی پتانسیل ها و میدان های الکتریکی را باید با روشی غیر از یافتن چگالی بار . یک مثال معمول این است که فرض کنیم الکترون ها رابطه بولتزمن :

n ه ∝ ه ه فی / ک ب تی ه . {\displaystyle n_{\text{e}}\propto e^{e\Phi /k_{\text{B}}T_{\text{e}}}.}

متمایز کردن این رابطه وسیله ای برای محاسبه میدان الکتریکی از چگالی فراهم می کند:

E = – ک ب تی ه ه ∇ n ه n ه . {\displaystyle \mathbf {E} =-{\frac {k_{\text{B}}T_{\text{e}}}{e}}{\frac {\nabla n_{\text{e}}} {n_{\text{e}}}}.}

(∇ عملگر گرادیان برداری است؛ nabla و گرادیان .)

ممکن است پلاسمایی تولید شود که شبه خنثی نباشد. برای مثال یک پرتو الکترونی فقط بارهای منفی دارد. چگالی یک پلاسمای غیر خنثی معمولاً باید بسیار کم باشد یا باید بسیار کوچک باشد. دافعه الکترواستاتیک آن را از بین می برد.

در اخترفیزیکی پلاسمای غربالگری Debye از تأثیر مستقیم میدان های الکتریکی بر پلاسما در فواصل زیاد، یعنی بیشتر از طول Debye می کند. با این حال، وجود ذرات باردار باعث می شود که پلاسما میدان های مغناطیسی . این می‌تواند رفتار بسیار پیچیده‌ای ایجاد کند، مانند تولید لایه‌های دوگانه پلاسما، جسمی که بار را در چند ده طول Debye می‌کند. دینامیک پلاسما در تعامل با میدان های مغناطیسی خارجی و خود تولید شده در رشته دانشگاهی مگنتوهیدرودینامیک .

پلاسما معمولاً چهارمین حالت ماده بعد از جامد، مایع و گاز نامیده می شود. [19] [20] از این حالت‌ها و دیگر حالات ماده . گرچه ارتباط نزدیکی با فاز گاز دارد، زیرا شکل یا حجم مشخصی نیز ندارد، اما از طرق مختلفی متفاوت است،

از جمله موارد زیر:

ویژگی گاز پلاسما
رسانایی الکتریکی بسیار کم: هوا یک عایق عالی است تا زمانی که در شدت میدان الکتریکی بالای 30 کیلو ولت بر سانتی متر به پلاسما تجزیه شود. [21] معمولاً بسیار زیاد: برای بسیاری از اهداف، رسانایی پلاسما ممکن است بی نهایت در نظر گرفته شود.
گونه هایی که به طور مستقل عمل می کنند یک: همه ذرات گاز به روشی مشابه رفتار می کنند، تحت تأثیر گرانش و برخورد با یکدیگر. دو یا سه: الکترون‌ها ، یون‌ها ، پروتون‌ها و نوترون‌ها را می‌توان با علامت و مقدار بار داد، به طوری که در بسیاری از شرایط، با سرعت‌های توده‌ای و دماهای مختلف، به طور مستقل رفتار می‌کنند و امکان بروز پدیده‌هایی مانند انواع جدید امواج و ناپایداری‌ها را فراهم می‌کنند.
توزیع سرعت ماکسولین : برخوردها معمولاً منجر به توزیع سرعت ماکسولی در تمام ذرات گاز می‌شوند، با ذرات نسبتاً سریع بسیار کمی. اغلب غیر ماکسولی: فعل و انفعالات برخوردی اغلب در پلاسمای داغ ضعیف هستند و فشار خارجی می تواند پلاسما را از تعادل محلی دور کند و منجر به جمعیت قابل توجهی از ذرات سریع غیرمعمول شود.
فعل و انفعالات باینری: برخورد دو ذره یک قانون است، برخورد سه جسم بسیار نادر است. جمعی: امواج یا حرکت سازمان یافته پلاسما بسیار مهم هستند زیرا ذرات می توانند در بردهای طولانی از طریق نیروهای الکتریکی و مغناطیسی برهم کنش داشته باشند.

مقاومت و رسانایی مواد مختلف

مقاله اصلی: مقاومت الکتریکی عناصر (صفحه داده)
  • رسانایی مانند فلز دارای رسانایی بالا و مقاومت کم است.
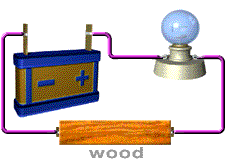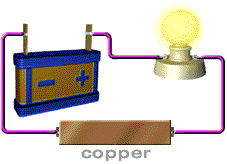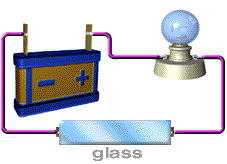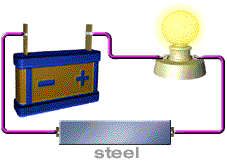
  • و عایق مانند شیشه مقاومت بالایی دارد.
  • رسانایی یک نیمه هادی عموماً متوسط ​​است، اما در شرایط مختلف، مانند قرار گرفتن مواد در معرض میدان های الکتریکی یا فرکانس های خاص نور ، و مهمتر از همه، با دما و ترکیب مواد نیمه هادی، بسیار متفاوت است.

درجه دوپینگ نیمه هادی ها تفاوت زیادی در رسانایی ایجاد می کند. تا حدی، دوپینگ بیشتر منجر به رسانایی بالاتر می شود. رسانایی محلول آب شوند به شدت به غلظت محلول آن نمک های و سایر گونه های شیمیایی که یونیزه در محلول رسانایی الکتریکی نمونه‌های آب به‌عنوان نشانگر میزان عاری از نمک، بدون یون یا عاری از ناخالصی نمونه استفاده می‌شود. هرچه آب خالص تر باشد، رسانایی کمتر است (مقاومت بیشتر). اندازه گیری رسانایی در آب اغلب به عنوان رسانایی خاص ، نسبت به رسانایی آب خالص در دمای 25 درجه سانتیگراد می شود. . EC متر معمولاً برای اندازه گیری رسانایی در محلول استفاده می شود خلاصه تقریبی به شرح زیر است:

مقاومت طبقاتی از مواد
مواد مقاومت، ρ (Ω · m)
ابررساناها 0
فلزات _ 10-8
نیمه هادی ها متغیر
الکترولیت ها متغیر
عایق ها 10 16
ابر عایق ها ∞

این جدول مقاومت ( ρ )، هدایت و ضریب دمایی مواد مختلف را در دمای 20 درجه سانتی گراد (68 درجه فارنهایت؛ 293 کلوین) نشان می دهد.

مقاومت، هدایت و ضریب دما برای چندین ماده
مواد مقاومت، ρ ،
در 20 درجه سانتی گراد (Ω·m)		 رسانایی، σ ،
در 20 درجه سانتی گراد (S/m)		 درجه حرارت
ضریب [c] (K -1 )		 ارجاع
نقره [d] 1.59 × _ 10-8 6.30 × 10 7 3.80 × 10-3 _ [22] [23]
مس [e] 1.68 × _ 10-8 5.96 × 10 7 4.04 × 10-3 _ [24] [25]
آنیل شده مس [f] 1.72 × _ 10-8 5.80 × 10 7 3.93 × 10-3 _ [26]
طلا [g] 2.44 × _ 10-8 4.11 × 10 7 3.40 × 10-3 _ [22]
آلومینیوم [h] 2.65 × _ 10-8 3.77 × 10 7 3.90 × 10-3 _ [22]
کلسیم 3.36 × _ 10-8 2.98 × 10 7 4.10 × 10-3 _
تنگستن 5.60 × _ 10-8 1.79 × 10 7 4.50 × 10-3 _ [22]
فلز روی 5.90 × _ 10-8 1.69 × 10 7 3.70 × 10-3 _ [27]
کبالت [i] 6.24 × _ 10-8 1.60 × 10 7 7.00 × 10-3 29 ]
[ منبع نامعتبر؟ ]
نیکل 6.99 × _ 10-8 1.43 × 10 7 6.00 × 10-3 _
روتنیوم [i] 7.10 × _ 10-8 1.41 × 10 7
لیتیوم 9.28 × _ 10-8 1.08 × 10 7 6.00 × 10-3 _
اهن 9.70 × _ 10-8 1.03 × 10 7 5.00 × 10-3 _ [22]
پلاتین 10.6 × _ 10-8 9.43 × 10 6 3.92 × 10-3 _ [22]
قلع 10.9 × _ 10-8 9.17 × 10 6 4.50 × 10-3 _
گالیوم 14.0 × _ 10-8 7.10 × 10 6 4.00 × 10-3 _
نیوبیم 14.0 × _ 10-8 7.00 × 10 6 [30]
فولاد کربنی (1010) 14.3 × _ 10-8 6.99 × 10 6 [31]
رهبری 22.0 × _ 10-8 4.55 × 10 6 3.90 × 10-3 _ [22]
گالینستان 28.9 × _ 10-8 3.46 × 10 6 [32]
تیتانیوم 42.0 × _ 10-8 2.38 × 10 6 3.80 × 10-3 _
دانه گرا فولاد الکتریکی 46.0 × _ 10-8 2.17 × 10 6 [33]
منگانین 48.2 × _ 10-8 2.07 × 10 6 0.002 × 10-3 _ [34]
کنستانتان 49.0 × _ 10-8 2.04 × 10 6 0.008 × 10-3 _ [35]
فولاد ضد زنگ [j] 69.0 × _ 10-8 1.45 × 10 6 0.94 × 10-3 _ [36]
سیاره تیر 98.0 × _ 10-8 1.02 × 10 6 0.90 × 10-3 _ [34]
منگنز 144 × _ 10-8 6.94 × 10 5
نیکروم [k] 110 × _ 10-8 6.70 × 10 5
[ نیازمند منبع ]		 0.40 × 10-3 _ [22]
کربن (گرافیت)
موازی با صفحه پایه [l]		 250 × _ 10-8 تا 500 × _ 10-8 2 × 10 5 تا 3 × 10 5
[ نیازمند منبع ]		 [4]
کربن (بی شکل) 0.5 × 10-3 _ تا 0.8 × 10-3 _ 1.25 × 10 3 تا 2.00 × 10 3 0.50 × 10 −3 [22] [37]
کربن (گرافیت)
عمود بر صفحه پایه		 3.0 × 10-3 _ 3.3 × 10 2 [4]
GaAs 10 10-3 تا _ 8
[ توضیح لازم است ]		 10 10-8 تا _ 3
[ مشکوک – بحث ]		 [38]
ژرمانیوم [m] 4.6 × 10-1 _ 2.17 -48.0 × 10-3 _ [22] [23]
آب دریا [n] 2.1 × 10-1 _ 4.8 [39]
آب استخر [o] 3.3 × 10-1 _ تا 4.0 × 10-1 _ 0.25 تا 0.30 [40]
آب آشامیدنی [p] 2 × 10 1 تا 2 × 10 3 5 × 10-2 10-4 تا 5 × _ _ [ نیازمند منبع ]
سیلیکون [m] 2.3 × 10 3 4.35 × _ 10-4 -75.0 × 10-3 _ [41] [22]
چوب (نم) 10 3 تا 10 4 _ 10-4 تا 10-3 _ [42]
آب دیونیزه [q] 1.8 × 10 5 4.2 × 10-5 _ [43]
شیشه 10 11 تا 10 15 10-15 _ تا _ 10-11 [22] [23]
کربن (الماس) 10 12 ~ _ 10-13 [44]
لاستیک سخت 10 13 _ 10-14 [22]
هوا 10 9 تا 10 15 ~ 10-15 _ تا _ 10-9 [45] [46]
چوب (خشک در فر) 10 14 تا 10 16 _ 10-16 تا _ 10-14 [42]
گوگرد 10 15 _ 10-16 [22]
کوارتز ذوب شده 7.5 × 10 17 1.3 × _ 10-18 [22]
PET 10 21 _ 10-21
PTFE (تفلون) 10 23 تا 10 25 _ 10-25 تا _ 10-23

ضریب دمای موثر با درجه حرارت و درجه خلوص مواد متفاوت است. مقدار 20 درجه سانتیگراد فقط زمانی که در دماهای دیگر استفاده می شود تقریبی است. به عنوان مثال، ضریب در دماهای بالاتر برای مس کمتر می شود و مقدار 0.00427 معمولاً در دمای 0 درجه سانتی گراد.

مقاومت بسیار کم (رسانایی بالا) نقره مشخصه فلزات است.

جورج گامو ماهیت برخورد فلزات با الکترون ها را در کتاب علمی محبوب خود یک، دو، سه… بی نهایت (1947) به طور مرتب خلاصه کرد:

تفاوت مواد فلزی با سایر مواد به این دلیل است که لایه‌های بیرونی اتم‌هایشان نسبتاً سست به هم متصل می‌شوند و اغلب باعث می‌شوند یکی از الکترون‌هایشان آزاد شود. بنابراین فضای داخلی یک فلز با تعداد زیادی الکترون غیر متصل پر شده است که مانند انبوهی از افراد آواره بی هدف به اطراف سفر می کنند. هنگامی که یک سیم فلزی در معرض نیروی الکتریکی اعمال شده بر روی انتهای مخالف آن قرار می گیرد، این الکترون های آزاد به سمت نیرو حرکت می کنند و در نتیجه جریان الکتریکی را تشکیل می دهند.

از نظر فنی تر، مدل الکترون آزاد توصیفی اساسی از جریان الکترون در فلزات ارائه می دهد.

می شود، اما مقاومت آن به شدت به میزان رطوبت بستگی دارد، به طوری که چوب مرطوب حداقل 1010 گرفته عایق بدتر از عایق خشک در فر است. [42] در هر صورت، یک ولتاژ به اندازه کافی بالا – مانند ولتاژ در صاعقه یا برخی از خطوط برق با فشار بالا – می تواند منجر به خرابی عایق و خطر برق گرفتگی حتی با چوب ظاهراً خشک شود. [ نیازمند منبع ]

وابستگی به دما

تقریب خطی

مقاومت الکتریکی اکثر مواد با دما تغییر می کند. اگر دمای T زیاد تغییر نکند، معمولاً از یک تقریب خطی استفاده می شود:

ρ ( تی ) = ρ 0 [ 1 + آ ( تی – تی 0 ) ] {\displaystyle \rho (T)=\rho _{0}[1+\alpha (T-T_{0})]}

 

جایی که آ {\displaystyle \alpha } نامیده می شود ضریب مقاومت ، تی 0 {\displaystyle T_{0}} یک دمای مرجع ثابت است (معمولا دمای اتاق)، و ρ 0 {\displaystyle \rho _{0}} مقاومت در دما است تی 0 {\displaystyle T_{0}} . پارامتر آ {\displaystyle \alpha } یک پارامتر تجربی برازش داده‌های اندازه‌گیری است ، برابر با 1/ ک {\displaystyle \kappa } [ شفاف سازی ] . از آنجا که تقریب خطی فقط یک تقریب است، آ {\displaystyle \alpha } برای دماهای مرجع مختلف متفاوت است. به همین دلیل معمولاً دمایی را که آ {\displaystyle \alpha } در با پسوند اندازه گیری شد، مانند آ 15 {\displaystyle \alpha _{15}} ، و این رابطه فقط در محدوده ای از دماهای اطراف مرجع برقرار است. [48] ​​هنگامی که دما در یک محدوده دمایی بزرگ تغییر می‌کند، تقریب خطی ناکافی است و باید از تحلیل و درک دقیق‌تری استفاده کرد.

فلزات

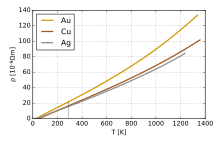
همچنین ببینید: دمای بلوخ-گرونایزن و مدل الکترون آزاد § میانگین مسیر آزاد

وابستگی مقاومت مقاومت طلا، مس و نقره به دما.

به طور کلی مقاومت الکتریکی فلزات با افزایش دما افزایش می یابد. الکترون و فونون می توانند نقش کلیدی ایفا کنند. در دماهای بالا، مقاومت یک فلز به صورت خطی با دما افزایش می یابد. با کاهش دمای یک فلز، وابستگی مقاومت به دما از تابع قانون توان دما پیروی می کند. از نظر ریاضی، وابستگی دمایی مقاومت ρ یک فلز را می توان از طریق فرمول بلوخ-گرونایزن تقریب زد: [49]

 

ρ ( تی ) = ρ ( 0 ) + آ ( تی Θ آر ) n 🔻 0 Θ آر / تی ایکس n ( ه ایکس – 1 ) ( 1 – ه – ایکس ) د ایکس {\displaystyle \rho (T)=\rho (0)+A\left({\frac {T}{\Theta _{R}}}\right)^{n}\int _{0}^{\ تتا _{R}/T}{\frac {x^{n}}{(e^{x}-1)(1-e^{-x})}}\,dx}

 

جایی که ρ ( 0 ) {\displaystyle \rho (0)} مقاومت باقیمانده ناشی از پراکندگی نقص است، A ثابت است که به سرعت الکترون ها در سطح فرمی ، شعاع دبای و چگالی عددی الکترون ها در فلز بستگی دارد. Θ آر {\displaystyle \Theta _{R}} است دمای دبی که از اندازه گیری های مقاومت به دست می آید و بسیار نزدیک با مقادیر دمای دبای به دست آمده از اندازه گیری های حرارتی خاص مطابقت دارد. n یک عدد صحیح است که به ماهیت تعامل بستگی دارد:

  • n = 5 نشان می دهد که مقاومت به دلیل پراکندگی الکترون ها توسط فونون ها است (مانند فلزات ساده).
  • n = 3 نشان می دهد که مقاومت به دلیل پراکندگی الکترون sd است (همانطور که در مورد فلزات واسطه وجود دارد)
  • n = 2 نشان می دهد که مقاومت به دلیل برهمکنش الکترون-الکترون است.

فرمول بلوخ-گرونایزن تقریبی است که با این فرض به دست می‌آید که فلز مورد مطالعه دارای سطح فرمی کروی است که در اولین منطقه بریلوین و یک طیف فونون دبای قرار دارد. [50]

اگر بیش از یک منبع پراکندگی به طور همزمان وجود داشته باشد، قانون ماتیسن (اولین بار توسط آگوستوس ماتیسن در دهه 1860 فرموله شد) [51] [52] بیان می کند که مقاومت کل را می توان با جمع کردن چندین عبارت مختلف تقریب زد، که هر کدام مقدار مناسبی دارند. n _

از آنجایی که دمای فلز به اندازه کافی کاهش می یابد (به طوری که تمام فونون ها منجمد می شوند)، مقاومت معمولاً به یک مقدار ثابت می رسد که به عنوان مقاومت باقی مانده . این مقدار نه تنها به نوع فلز، بلکه به خلوص و تاریخچه حرارتی آن بستگی دارد. مقدار مقاومت باقیمانده یک فلز با غلظت ناخالصی آن تعیین می شود. برخی از مواد تمام مقاومت الکتریکی خود را در دماهای به اندازه کافی پایین از دست می دهند، به دلیل اثری به نام ابررسانایی .

تحقیق در مورد مقاومت فلزات در دمای پایین انگیزه هایک کامرلینگ اونس بود که در سال 1911 منجر به کشف ابررسانایی شد. برای جزئیات بیشتر به تاریخچه ابررسانایی .

قانون Wiedemann-Franz

قانون Wiedemann-Franz بیان می کند که ضریب هدایت الکتریکی فلزات در دمای معمولی با دما نسبت معکوس دارد: [53]

σ ∼ 1 تی . {\displaystyle \sigma \thicksim {1 \over T}.}

در دماهای بالای فلز، قانون ویدمان-فرانتس چنین است:

ک σ = پی 2 3 ( ک ه ) 2 تی ، {\displaystyle {K \over \sigma }={\pi ^{2} \over 3}\left({\frac {k}{e}}\right)^{2}T,}

جایی که ک {\ displaystyle K} هدایت حرارتی فلز است، ک {\ displaystyle k} ثابت بولتزمن است ، ه {\displaystyle e} بار الکترون است، تی {\displaystyle T} دما است و σ {\displaystyle \sigma } ضریب هدایت الکتریکی است.

نیمه هادی ها

نوشتار اصلی: نیمه هادی

به طور کلی، ذاتی نیمه هادی با افزایش دما کاهش می یابد. الکترون‌ها نوار انرژی رسانایی ، جایی که آزادانه جریان می‌یابند، و با انجام این کار، حفره‌هایی در نوار ظرفیت که آزادانه نیز جریان دارند. مقاومت الکتریکی یک ذاتی (غیر دوپ) نیمه هادی کاهش طور تصاعدی با دما به

ρ = ρ 0 ه – آ تی {\ displaystyle \ rho = \ rho _ {0} e ^ {- aT} \,}

یک تقریب حتی بهتر از وابستگی دمایی مقاومت یک نیمه هادی توسط معادله استاینهارت-هارت به دست می :

1 تی = آ + ب لوگاریتم ⁡ ρ + سی ( لوگاریتم ⁡ ρ ) 3 {\displaystyle {\frac {1}{T}}=A+B\ln \rho +C(\ln \rho )^{3}}

که در آن A ، B و C به اصطلاح ضرایب Steinhart-Hart هستند.

از این معادله برای کالیبره کردن ترمیستورها .

نیمه هادی های بیرونی (دوپ شده) مشخصات دمایی بسیار پیچیده تری دارند. با افزایش دما که از صفر مطلق شروع می شود، ابتدا مقاومت آنها به شدت کاهش می یابد زیرا حامل ها اهدا کنندگان یا پذیرندگان را ترک می کنند. پس از اینکه اکثر اهداکنندگان یا پذیرندگان حامل های خود را از دست دادند، مقاومت مجدداً به دلیل کاهش تحرک حامل ها (مثل یک فلز) کمی افزایش می یابد. در دماهای بالاتر، آنها مانند نیمه هادی های ذاتی رفتار می کنند زیرا حامل ها از دهنده ها/پذیرنده ها در مقایسه با حامل های حرارتی ناچیز می شوند. [54]

در نیمه هادی های غیر کریستالی، رسانایی می تواند با تونل کوانتومی از یک مکان محلی به مکان دیگر رخ دهد. این به عنوان پرش دامنه متغیر و شکل مشخصه ای دارد

ρ = آ انقضا ⁡ ( تی – 1 n ) ، {\displaystyle \rho =A\exp \left(T^{-{\frac {1}{n}}}\راست)،}

که در آن n = 2، 3، 4، بسته به ابعاد سیستم.

مقاومت و رسانایی پیچیده

هنگام تجزیه و تحلیل پاسخ مواد به میدان های الکتریکی متناوب ( طیف سنجی دی الکتریک )، [55] در کاربردهایی مانند توموگرافی امپدانس الکتریکی ، [56] راحت است پیچیده ای کمیت مقاومت (در قیاس با امپدانس الکتریکی . Impedivity مجموع یک جزء واقعی، مقاومت، و یک جزء خیالی، واکنش (در قیاس با راکتانس ) است. قدر مقاومت جذر مجموع مجذورهای قدر مقاومت و واکنش پذیری است.

برعکس، در چنین مواردی رسانایی باید به صورت یک عدد مختلط (یا حتی به صورت ماتریسی از اعداد مختلط، در مورد ناهمسانگرد ) بیان . پذیرش مجموع یک جزء واقعی به نام رسانایی و یک جزء خیالی به نام حساسیت است.

یک توصیف جایگزین از پاسخ به جریان های متناوب از یک رسانایی واقعی (اما وابسته به فرکانس) همراه با گذردهی کند. هر چه رسانایی بزرگتر باشد، سیگنال جریان متناوب سریعتر توسط ماده جذب می شود (یعنی ماده مات است). برای جزئیات، به توضیحات ریاضی کدورت کنید.

مقاومت در برابر مقاومت در هندسه های پیچیده

حتی اگر مقاومت ماده مشخص باشد، محاسبه مقاومت ماده ساخته شده از آن ممکن است در برخی موارد بسیار پیچیده تر از فرمول باشد. آر = ρ ℓ / آ {\ displaystyle R = \ rho \ ell / A} در بالا. یک مثال، پروفیل مقاومتی گسترش ، که در آن مواد ناهمگن هستند (مقاومت متفاوت در مکان‌های مختلف)، و مسیرهای دقیق جریان جریان مشخص نیست.

در مواردی مانند این، فرمول ها

جی = σ E ⇌ E = ρ جی {\displaystyle J=\sigma E\,\,\\,\,E=\rho J}

باید جایگزین شود

جی ( r ) = σ ( r ) E ( r ) ⇌ E ( r ) = ρ ( r ) جی ( r ) ، {\displaystyle \mathbf {J} (\mathbf {r} )=\sigma (\mathbf {r} )\mathbf {E} (\mathbf {r} )\,\,\\,\,\mathbf { E} (\mathbf {r} )=\rho (\mathbf {r} )\mathbf {J} (\mathbf {r})،}

که در آن E و J اکنون فیلدهای برداری هستند . این معادله، همراه با معادله پیوستگی برای J و معادله پواسون برای E ، مجموعه ای از معادلات دیفرانسیل جزئی . در موارد خاص، یک راه حل دقیق یا تقریبی برای این معادلات را می توان با دست انجام داد، اما برای پاسخ های بسیار دقیق در موارد پیچیده، ممکن است به روش های کامپیوتری مانند تجزیه و تحلیل اجزای محدود نیاز باشد.

محصول مقاومت-چگالی

در برخی کاربردها که وزن یک آیتم بسیار مهم است، حاصلضرب مقاومت و چگالی مهمتر از مقاومت کم مطلق است – اغلب ممکن است رسانا را ضخیم تر کرد تا مقاومت بالاتری را جبران کرد. و سپس یک ماده محصول با چگالی مقاومت پایین (یا معادل آن نسبت رسانایی به چگالی بالا) مطلوب است. مسافت طولانی خطوط برق هوایی ، آلومینیوم اغلب به جای مس (Cu) استفاده می شود، زیرا برای رسانایی یکسان سبک تر است.

نقره، اگرچه کم مقاومت ترین فلز شناخته شده است، چگالی بالایی دارد و با این اندازه عملکردی مشابه مس دارد، اما بسیار گران تر است. کلسیم و فلزات قلیایی دارای بهترین محصولات با چگالی مقاومت هستند، اما به دلیل واکنش پذیری بالا با آب و اکسیژن (و کمبود قدرت فیزیکی) به ندرت برای رساناها استفاده می شوند. آلومینیوم به مراتب پایدارتر است. سمیت انتخاب بریلیم را حذف می کند. [57] (بریلیم خالص نیز شکننده است.) بنابراین، زمانی که وزن یا هزینه یک هادی در نظر گرفته شود، معمولاً آلومینیوم فلز انتخابی است.

مقاومت، چگالی و محصولات چگالی مقاومتی مواد انتخاب شده
مواد مقاومت
( nΩ·m )		 تراکم
( گرم / سانتی متر 3 )		 مقاومت × چگالی …، نسبت به مس ، دادن
هدایت مشابه		 قیمت تقریبی، در
9 دسامبر 2018 [ نیازمند منبع ]
( g·mΩ/ m2 ) نسبت فامیلی
به مس 		جلد جرم (دلار آمریکا به ازای هر کیلوگرم) نسبت به مس
سدیم 47.7 0.97 46 31% 2.843 0.31
لیتیوم 92.8 0.53 49 33% 5.531 0.33
کلسیم 33.6 1.55 52 35% 2.002 0.35
پتاسیم 72.0 0.89 64 43% 4.291 0.43
بریلیم 35.6 1.85 66 44% 2.122 0.44
آلومینیوم 26.50 2.70 72 48% 1.5792 0.48 2.0 0.16
منیزیم 43.90 1.74 76 51% 2.616 0.51
مس 16.78 8.96 150 100% 1 1 6.0 1
نقره 15.87 10.49 166 111% 0.946 1.11 456 84
طلا 22.14 ساعت 19.30 427 285% 1.319 2.85 39000 19000
اهن 96.1 7.874 757 505% 5.727 5.05

همچنین مشاهده کنید

  • مکانیسم های انتقال بار
  • کمایریستور
  • طبقه بندی مواد بر اساس گذردهی
  • رسانایی نزدیک به آستانه نفوذ
  • مقاومت تماسی
  • مقاومت الکتریکی عناصر (صفحه داده)
  • توموگرافی مقاومت الکتریکی
  • مقاومت ورق
  • واحدهای الکترومغناطیس SI
  • اثر پوستی
  • مقاومت اسپیتزر

یادداشت ها

  • عدد اتمی تعداد الکترون‌های اتمی است که از نظر الکتریکی خنثی است – بار الکتریکی خالص ندارد.
  • مرتبط که به طور خاص در نظر گرفته نمی شوند، اندازه کل کریستال و عوامل خارجی محیط اطراف است که نوارهای انرژی را تغییر می دهند، مانند میدان های الکتریکی یا مغناطیسی تحمیلی.
  • اعداد در این ستون، معنی دار مقاومت را افزایش یا کاهش می دهند. به عنوان مثال، در دمای 30 درجه سانتیگراد (303 کلوین)، مقاومت نقره × 10-8 است 1.65 . این به صورت Δ 0 = α Δρ T ρ محاسبه که ρ 0 مقاومت در 20 درجه سانتی گراد (در این مورد) و α ضریب دما است.
  • رسانایی نقره فلزی برای اکثر اهداف عملی به طور قابل توجهی بهتر از مس فلزی نیست – تفاوت بین این دو را می توان به راحتی با ضخیم کردن سیم مسی تنها به میزان 3٪ جبران کرد. با این حال، نقره برای نقاط تماس الکتریکی در معرض نور ترجیح داده می شود، زیرا خورده یک رسانای قابل تحمل است، اما مس خورده، مانند اکثر فلزات خورده، عایق نسبتا خوبی است.
  • مس به طور گسترده در تجهیزات الکتریکی، سیم کشی ساختمان و کابل های مخابراتی استفاده می شود.
  • به عنوان 100% IACS یا استاندارد بین المللی مس آنیل می شود. واحدی برای بیان رسانایی مواد غیر مغناطیسی با آزمایش با استفاده از جریان گردابی . به طور کلی برای تأیید مزاج و آلیاژ آلومینیوم استفاده می شود.
  • علیرغم اینکه رسانایی کمتری نسبت به مس دارد، طلا معمولاً در تماس های الکتریکی زیرا به راحتی خورده نمی شود.
  • معمولا برای خطوط برق هوایی با فولاد تقویت شده (ACSR)
  • کبالت و روتنیوم جایگزین مس در مدارهای مجتمع ساخته شده در گره های پیشرفته هستند [28]
  • 18% کروم و 8% نیکل فولاد زنگ نزن آستنیتی
  • آلیاژ نیکل – آهن – کروم که معمولاً در عناصر گرمایشی استفاده می شود.
  • گرافیت به شدت ناهمسانگرد است.
  • مقاومت نیمه هادی ها به شدت به وجود ناخالصی ها در ماده بستگی دارد.
  • مربوط به شوری متوسط ​​35 گرم بر کیلوگرم در 20 درجه سانتیگراد است.
  • pH باید حدود 8.4 و رسانایی در محدوده 2.5-3 mS/cm باشد. مقدار کمتر برای آب تازه تهیه شده مناسب است. رسانایی برای تعیین TDS (کل ذرات محلول) استفاده می شود.
  • این محدوده مقدار برای آب آشامیدنی با کیفیت معمولی است و نشانگر کیفیت آب نیست
  1. رسانایی با گازهای تک اتمی موجود کمترین است. به 12 × 10-5 گاززدایی یا 7.5 × 10-5 به در صورت تعادل در جو به دلیل CO2 محلول با

منابع

  • لوری، ویلیام (2007). مبانی ژئوفیزیک . انتشارات دانشگاه کمبریج. صص 254-55. شابک  978-05-2185-902-8 . بازبینی شده در 24 مارس 2019 .
  • کومار، ناریندر (2003). فیزیک جامع برای کلاس دوازدهم . دهلی نو: انتشارات لاکسمی. صص 280-84. شابک  978-81-7008-592-8 . بازبینی شده در 24 مارس 2019 .
  • بوگاتین، اریک (2004). یکپارچگی سیگنال: ساده شده پرنتیس هال حرفه ای. پ. 114. شابک  978-0-13-066946-9 . بازبینی شده در 24 مارس 2019 .
  • هیو او. پیرسون، کتابچه راهنمای کربن، گرافیت، الماس، و فولرن ها: خواص، پردازش، و کاربردها ، ص. 61، ویلیام اندرو، 1993 شابک  0-8155-1339-9 .
  • JR Tyldesley (1975) مقدمه ای بر تحلیل تانسور: برای مهندسان و دانشمندان کاربردی ، لانگمن، شابک  0-582-44355-5
  • G. Woan (2010) The Cambridge Handbook of Physics Formulas , انتشارات دانشگاه کمبریج، شابک  978-0-521-57507-2
  • جوزف پک، توماس ورنر (3 آوریل 2007). “مدل سازی تفاضل محدود میدان های مغناطیسی تلوریک در محیط های ناهمسانگرد دو بعدی” . مجله بین المللی ژئوفیزیک . 128 (3): 505-521. doi : 10.1111/j.1365-246X.1997.tb05314.x .
  • دیوید تانگ (ژانویه 2016). “اثر سالن کوانتومی: سخنرانی های TIFR Infosys” (PDF) . بازیابی شده در 14 سپتامبر 2018 .
  • کساپ، صفا; کوغیا، سیریل؛ رودا، هری ای. (2017). “رسانایی الکتریکی در فلزات و نیمه هادی ها” (PDF) . کتاب پرینگر مواد الکترونیکی و فوتونیک . صفا کاسپ، سیریل کوغیا، هری ای رودا . پ. 1. doi : 10.1007/978-3-319-48933-9_2 . شابک  978-3-319-48931-5 .
  • پیوند (sl) . ibchem.com
  • “جریان در مقابل سرعت دریفت” . فیزیک درس بازبینی شده در 20 اوت 2014 .
  • لو، داگ (2012). الکترونیک همه در یک برای آدمک ها . جان وایلی و پسران شابک  978-0-470-14704-7 .
  • کیت ولش “پرسش و پاسخ – مقاومت الکتریکی را چگونه توضیح می دهید؟” . ملی توماس جفرسون دهنده بازبینی شده در 28 آوریل 2017 .
  • “Electromigration: Electromigration چیست؟” . دانشگاه فنی خاورمیانه . بازبینی شده در 31 جولای 2017 . هنگامی که الکترون ها از طریق یک فلز هدایت می شوند، با عیوب در شبکه برهم کنش می کنند و پراکنده می شوند. […] انرژی حرارتی با ایجاد ارتعاش اتم ها باعث ایجاد پراکندگی می شود. این منبع مقاومت فلزات است.
  • فابر، تی (1972). مقدمه ای بر تئوری فلزات مایع . انتشارات دانشگاه کمبریج. شابک  9780521154499 .
  • “سخنرانی های فاینمن در فیزیک، جلد سوم، فصل 21: معادله شرودینگر در زمینه کلاسیک: سمیناری در مورد ابررسانایی” . بازبینی شده در 26 دسامبر 2021 .
  • جان سی گالوپ (1990). SQUIDS، اثرات جوزفسون و الکترونیک ابررسانا . CRC را فشار دهید . ص 3، 20. شابک  978-0-7503-0051-3 .
  • رجوع کنید به فلش در آسمان: انفجار پرتو گامای زمین توسط رعد و برق ایجاد می شود
  • Yaffa Eliezer، Shalom Eliezer، The Fourth State of Matter: An Introduction to Physics of Plasma ، ناشر: Adam Hilger، 1989، ISBN  978-0-85274-164-1 ، 226 صفحه، صفحه 5
  • Bittencourt، JA (2004). مبانی فیزیک پلاسما . اسپرینگر. پ. 1. ISBN  9780387209753 .
  • هانگ، آلیس (2000). “قدرت دی الکتریک هوا” . کتاب حقایق فیزیک .
  • Raymond A. Serway (1998). اصول فیزیک (ویرایش دوم). فورت ورث، تگزاس؛ لندن: انتشارات کالج ساندرز. پ. 602 . شابک  978-0-03-020457-9 .
  • دیوید گریفیث (1999) [1981]. “7 الکترودینامیک” . در آلیسون ریوز (ویرایش). مقدمه ای بر الکترودینامیک (ویرایش سوم). رودخانه فوقانی زین، نیوجرسی: سالن پرنتیس . پ. 286 . شابک  978-0-13-805326-0 . OCLC  40251748 .
  • Matula، RA (1979). “مقاومت الکتریکی مس، طلا، پالادیوم و نقره”. مجله داده های مرجع فیزیکی و شیمیایی . 8 (4): 1147. Bibcode : 1979JPCRD…8.1147M . doi : 10.1063/1.555614 . S2CID  95005999 .
  • داگلاس جیانکولی (2009) [1984]. “25 جریان الکتریکی و مقاومت”. در جوسلین فیلیپس (ویرایش). فیزیک برای دانشمندان و مهندسان با فیزیک مدرن (ویرایش چهارم). رودخانه فوقانی زین، نیوجرسی: سالن پرنتیس . پ. 658. شابک  978-0-13-149508-1 .”میزهای سیم مسی” . اداره ملی استاندارد ایالات متحده بازیابی شده در 3 فوریه 2014 – از طریق بایگانی اینترنتی – archive.org (بایگانی شده در 10-03-2001).
  • فیزیکی های (فرمت PDF؛ صفحه 2، جدول در گوشه پایین سمت راست را ببینید). بازیابی شده در 2011-12-17.
  • IITC – Imec نتایج اتصال مس، کبالت و روتنیم را ارائه می دهد
  • “ضریب مقاومت دمایی | یادداشت های الکترونیک” .خواص مواد نیوبیم.
  • AISI 1010 Steel، کشش سرد . مت وب
  • کارچر، چ. Kocourek, V. (دسامبر 2007). “ناپایداری های سطح آزاد در طول شکل دهی الکترومغناطیسی فلزات مایع” . PAMM . 7 (1): 4140009–4140010. doi : 10.1002/pamm.200700645 . ISSN  1617-7061 .

“فولاد JFE” (PDF) . بازیابی 2012-10-20 .

  • داگلاس سی جیانکولی (1995). فیزیک: اصول با کاربردها (ویرایش چهارم). لندن: پرنتیس هال. شابک  978-0-13-102153-2 .
    (همچنین به جدول مقاومت کنید. hyperphysics.phy-astr.gsu.edu)
  • جان اومالی (1992) طرح کلی تئوری شاوم و مسائل تحلیل مدار پایه ، ص. 19، McGraw-Hill Professional، شابک  0-07-047824-4
  • گلن الرت (ویرایش)، “مقاومت فولاد” ، کتاب حقایق فیزیک ، بازیابی و بایگانی شده در 16 ژوئن 2011.
  • Y. Pauleau, Péter B. Barna, PB Barna (1997) پوشش های محافظ و لایه های نازک: سنتز، خصوصیات و کاربردها ، ص. 215، اسپرینگر، شابک  0-7923-4380-8 .
  • میلتون اورینگ (1995). علم مواد مهندسی، جلد 1 (ویرایش سوم). مطبوعات دانشگاهی. پ. 561. شابک  978-0125249959 .
  • خواص فیزیکی آب دریا آرشیو شده 2018-01-18 در ماشین Wayback . Kayelaby.npl.co.uk. بازیابی شده در 2011-12-17.
  • [1] . chemistry.stackexchange.com
  • ارانا، گولا (2014). رشد کریستال و ارزیابی سیلیکون برای VLSI و ULSI . مطبوعات CRC. پ. 7. ISBN  978-1-4822-3281-3 .
  • داده خطوط انتقال . Transmission-line.net. بازبینی شده در 03/02/2014.
  • آر ام پشلی; M. Rzechowicz; LR Pashley; ام جی فرانسیس (2005). “آب بدون گاز پاک کننده بهتری است”. مجله شیمی فیزیک ب . 109 (3): 1231-8. doi : 10.1021/jp045975a . PMID  16851085 .
  • لارنس اس.پان، دان آر. کانیا، الماس: خواص و کاربردهای الکترونیکی ، ص. 140، اسپرینگر، 1994 شابک  0-7923-9524-7 .
  • اس دی پاوار; P. Murugavel; دی ام لال (2009). “تأثیر رطوبت نسبی و فشار سطح دریا بر هدایت الکتریکی هوا بر فراز اقیانوس هند” . مجله تحقیقات ژئوفیزیک . 114 (D2): D02205. Bibcode : 2009JGRD..114.2205P . doi : 10.1029/2007JD009716 .
  • E. Seran; M. Godefroy; ای پیلی (2016). “آنچه می توانیم از اندازه گیری رسانایی الکتریکی هوا در اتمسفر غنی از 222Rn بیاموزیم . علوم زمین و فضا . 4 (2): 91-106. Bibcode : 2017E&SS….4…91S . doi : 10.1002/2016EA000241 .
  • میزهای سیم مسی بایگانی شده در Wayback Machine . وزارت ایالات متحده بازرگانی دفترچه راهنمای دفتر ملی استاندارد. 21 فوریه 1966
  • وارد، مالکوم آر (1971). علم مهندسی برق . آموزش فنی مک گراو هیل. میدنهد، انگلستان: مک گراو هیل. صص 36-40. شابک  9780070942554 .
  • Grüneisen, E. (1933). “وابستگی مقاومت الکتریکی فلزات خالص به دما” . سالنامه فیزیک . 408 (5): 530-540. Bibcode : 1933AnP…408..530G . doi : 10.1002/andp.19334080504 . ISSN  1521-3889 .
  • نظریه کوانتومی مواد واقعی جیمز آر چلیکوفسکی، استیون جی لویی. بوستون: ناشران آکادمیک Kluwer. 1996. صفحات 219-250. شابک  0-7923-9666-9 . OCLC  33335083 .
  • A. Matthiessen، Rep. بریتانیایی الاغ 32, 144 (1862)
  • A. Matthiessen، Progg. Anal, 122, 47 (1864)
  • جونز، ویلیام؛ مارس، نورمن اچ (1985). فیزیک حالت جامد نظری . انتشارات دوور.
  • جی. سیمور (1972) الکترونیک فیزیکی ، فصل 2، پیتمن
  • استفنسون، سی. هابلر، ا. (2015). “پایداری و رسانایی سیم های خود مونتاژ شده در میدان الکتریکی عرضی” . علمی نماینده _ 5 : 15044. Bibcode : 2015NatSR…515044S . doi : 10.1038/srep15044 . PMC  4604515 . PMID  26463476 .
  • اتو اچ. اشمیت، دانشگاه مینه‌سوتا، طیف‌سنجی مقاومت متقابل و امکان ادغام آن در بازسازی تشریحی تشخیصی بافت و اندازه‌گیری‌های فیزیولوژیکی منسجم زمان . otto-schmitt.org. بازیابی شده در 2011-12-17.
  • “بریلیوم (Be) – خواص شیمیایی، سلامتی و اثرات زیست محیطی” .

رسانایی (الکترولیتی)

از ویکیپدیا، دانشنامه آزاد

پرش به پیمایش پرش به جستجو

رسانایی (یا رسانایی خاص ) الکترولیت معیاری برای سنجش توانایی آن در هدایت الکتریسیته است. واحد SI رسانایی زیمنس بر متر (S/m) است.

اندازه گیری رسانایی به طور معمول در بسیاری از کاربردهای صنعتی و محیطی به عنوان روشی سریع، ارزان و قابل اعتماد برای اندازه گیری محتوای یونی در محلول استفاده می شود. [1] به عنوان مثال، اندازه گیری هدایت محصول یک روش معمولی برای نظارت و روند مداوم عملکرد تصفیه آب است.

رسانایی الکترولیتی آب با خلوص فوق العاده بالا به دلیل تفکیک بیشتر آب به عنوان تابعی از دما (T) افزایش می یابد. H 2 O در  H + و  OH – با T.

در بسیاری از موارد، هدایت مستقیماً به کل جامدات محلول (TDS) مرتبط است. آب دیونیزه شده با کیفیت بالا دارای رسانایی در حدود 0.05 μS/cm در دمای 25 درجه سانتی گراد است، آب آشامیدنی معمولی در محدوده 200-800 μS/cm است، در حالی که آب دریا حدود 50 mS/cm [2] (یا 50,000 μS/ سانتی متر).

رسانایی به طور سنتی با اتصال الکترولیت در پل وتستون شود. محلول های رقیق از کولراوش در مورد وابستگی به غلظت و افزایش مشارکت های یونی پیروی می کنند. لارس اونساگر توضیحی نظری از قانون نظریه Debye-Hückel .

واحدها

واحد SI رسانایی S /m است و در غیر اینصورت به 25 درجه سانتیگراد اشاره دارد. به طور کلی، واحد سنتی μS/cm است.

سلول استاندارد معمولاً 1 سانتی متر عرض دارد و بنابراین برای آب بسیار خالص در تعادل با هوا مقاومتی در حدود 10 6 اهم دارد که به عنوان مگا . آب فوق خالص می تواند به ۱۸ مگا اهم یا بیشتر برسد. بنابراین در گذشته از megohm-cm استفاده می شد که گاهی اوقات به اختصار به “megohm” گفته می شد. گاهی اوقات، رسانایی در “microsiemens” (با حذف عبارت فاصله در واحد) داده می شود. در حالی که این یک خطا است، اغلب می توان آن را برابر با μS/cm سنتی فرض کرد.

تبدیل رسانایی به کل جامدات محلول بستگی به ترکیب شیمیایی نمونه دارد و می تواند بین 0.54 تا 0.96 متغیر باشد. به طور معمول، تبدیل با فرض اینکه جامد کلرید سدیم است انجام می شود. 1 μS/cm معادل حدود 0.64 میلی گرم NaCl به ازای هر کیلوگرم آب است.

رسانایی مولی دارای واحد SI S m 2 mol -1 است. انتشارات قدیمی‌تر از واحد Ω -1 سانتی‌متر 2 مول -1 استفاده می‌کنند.

اندازه گیری

مقاله اصلی: رسانایی سنج الکتریکی

اصل اندازه گیری

محلول رسانایی الکتریکی یک الکترولیت با تعیین مقاومت محلول بین دو الکترود شکل که با یک فاصله ثابت از هم جدا شده اند اندازه گیری می شود. [3] یک ولتاژ متناوب به طور کلی برای به حداقل رساندن الکترولیز . [ نیاز به منبع ] مقاومت با رسانایی متر اندازه گیری می شود . فرکانس‌های معمولی مورد استفاده در محدوده 1 تا 3 کیلوهرتز هستند. وابستگی به فرکانس معمولاً اندک است، [4] اما ممکن است در فرکانس‌های بسیار بالا قابل‌توجه باشد، اثری که به عنوان اثر Debye–Falkenhagen شناخته .

طیف گسترده ای از ابزار دقیق به صورت تجاری در دسترس است. [5] معمولاً از دو نوع حسگر الکترود استفاده می شود، حسگرهای مبتنی بر الکترود و حسگرهای القایی. حسگرهای الکترود با طراحی ایستا برای رسانایی کم و متوسط ​​مناسب هستند و در انواع مختلفی وجود دارند که دارای دو یا چهار الکترود هستند که در آن الکترودها می توانند برعکس، صاف یا در یک استوانه قرار گیرند. [6] سلول‌های الکترودی با طراحی انعطاف‌پذیر، که در آن فاصله بین دو الکترود با چیدمان مخالف می‌تواند متفاوت باشد، دقت بالایی ارائه می‌دهد و همچنین می‌تواند برای اندازه‌گیری رسانه‌های بسیار رسانا استفاده شود. [7] حسگرهای القایی برای شرایط سخت شیمیایی مناسب هستند اما به حجم نمونه بزرگتری نسبت به حسگرهای الکترود نیاز دارند. [8] سنسورهای رسانایی معمولاً با محلول های KCl با رسانایی شناخته شده کالیبره می شوند. رسانایی الکترولیتی به شدت وابسته به دما است، اما بسیاری از سیستم‌های تجاری اصلاح خودکار دما را ارائه می‌کنند. جداول رسانایی مرجع برای بسیاری از راه حل های رایج موجود است. [9]

تعاریف

مقاومت، R ، متناسب با فاصله، l ، بین الکترودها است و با سطح مقطع نمونه، A (به S در شکل بالا اشاره شده است). نوشتن ρ (rho) برای مقاومت خاص، یا مقاومت .

آر = ρ ل آ {\displaystyle R=\rho {\frac {l}{A}}}

در عمل سلول رسانایی کالیبره با استفاده از محلول‌هایی با مقاومت خاص شناخته شده، ρ* ، بنابراین کمیت‌های منفرد l و A نیازی به دانستن دقیق ندارند، بلکه فقط باید نسبت آنها را مشخص کرد. [10] اگر مقاومت محلول کالیبراسیون R * باشد، یک سلول ثابت است که به عنوان نسبت l و A ( C = l ⁄ A ) مشتق شده است.

آر ∗ = ρ × سی {\displaystyle R^{*}=\rho \times C}

رسانایی خاص (رسانایی)، κ (کاپا) متقابل مقاومت ویژه است.

ک = 1 ρ = سی آر {\displaystyle \kappa ={\frac {1}{\rho }}={\frac {C}{R}}}

رسانایی نیز وابسته به دما است . گاهی اوقات رسانایی (مقابله مقاومت) با G = 1 ⁄ R. _ سپس رسانایی خاص κ (کاپا) برابر است با:

ک = سی × جی {\displaystyle \kappa =C\times G}

نظریه

رسانایی ویژه محلولی حاوی یک الکترولیت به غلظت الکترولیت بستگی دارد. بنابراین، تقسیم رسانایی خاص بر غلظت راحت است. این ضریب، که رسانایی مولی ، با Λ m

Λ متر = ک ج display \ displaystyle \ Lambda _ {\ mathrm {m}} = fra \ frac {\ kappa} {c}

الکترولیت های قوی

الکترولیت های قوی فرض بر این است که تجزیه طور کامل در محلول رسانایی محلول یک الکترولیت قوی در غلظت کم از قانون Kohlrausch

Λ متر = Λ متر 0 – ک ج display \ displaystyle \ Lambda _ {\ mathrm {m}} = \ Lambda _ {\ mathrm {m} ^ {0} -K {\ sqrt {c}

جایی که Λ 0
m به عنوان هدایت مولی محدود شناخته می شود، K یک ثابت تجربی و c غلظت الکترولیت است. (محدود کردن در اینجا به معنای “در حد رقت نامتناهی” است.) در واقع، رسانایی مشاهده شده یک الکترولیت قوی مستقیماً با غلظت متناسب می شود، در غلظت های به اندازه کافی پایین، یعنی زمانی که

Λ متر 0 ≫ ک ج {\displaystyle \Lambda _{\mathrm {m} }^{0}\gg K{\sqrt {c}}}

با افزایش غلظت، رسانایی دیگر به نسبت افزایش نمی یابد. علاوه بر این، Kohlrausch همچنین دریافت که رسانایی محدود الکترولیت.

λ 0
+ و λ 0
– رسانایی مولی محدود کننده هر یون است.

جدول زیر مقادیری را برای رسانایی مولی محدود برای برخی یون های انتخاب شده ارائه می دهد. [11]

جدول محدودیت هدایت یونی در آب در دمای 298 K (تقریباً 25 درجه سانتیگراد) [11]
کاتیون ها λ 0
+ / mS m 2 mol -1		 کاتیون ها λ 0
+ / mS m 2 mol -1		 آنیون ها λ 0
– / mS m 2 mol -1		 آنیون ها λ 0
– / mS m 2 mol -1
H + 34.982 Ba 2+ 12.728 اوه – 19.8 SO 2-
4		 15.96
لی + 3.869 Mg 2+ 10.612 Cl – 7.634 سی
2 O 2-
4		 7.4
Na + 5.011 La 3+ 20.88 برادر – 7.84 HC
2 O –
4		 4.306 [12]
K + 7.352 Rb + 7.64 من – 7.68 HCOO – 5.6
NH +
4		 7.34 Cs + 7.68 نه –
3		 7.144 CO 2-
3		 7.2
Ag + 6.192 باشید 2+ 4.50 CH 3 COO – 4.09 HSO 2-
3		 5.0
Ca 2+ 11.90 ClO –
4		 6.80 SO 2-
3		 7.2
شرکت (کوچک)
3 ) 3+
6		 10.2 F – 5.50

تفسیری از این نتایج بر اساس نظریه دبای و هوکل بود که نظریه دبای-هوکل-آنساگر را به دست آورد: [13]

Λ متر = Λ متر 0 – ( آ + ب Λ متر 0 ) ج display \ displaystyle \ Lambda _ {\ mathrm {m}} = \ Lambda _ {\ mathrm {m} ^ {0} – \ left (A + B \ Lambda _ {\ mathrm {m} ^ 0 \ right) {\ sqrt {c

که در آن A و B ثابت هایی هستند که فقط به مقادیر شناخته شده مانند دما، بارهای روی یون ها و ثابت دی الکتریک و ویسکوزیته حلال بستگی دارند. همانطور که از نام آن پیداست، این بسط نظریه Debye-Hückel است ، به دلیل Onsager . برای محلول های با غلظت کم بسیار موفق است.

الکترولیت های ضعیف

الکترولیت ضعیف الکترولیتی است که هرگز به طور کامل تفکیک نمی شود (مخلوطی از یون ها و مولکول های کامل در حالت تعادل وجود دارد). در این مورد هیچ محدودیتی برای رقت وجود ندارد که در زیر آن رابطه بین هدایت و غلظت خطی شود. در عوض، محلول در غلظت‌های ضعیف‌تر به طور کامل تفکیک می‌شود، و برای غلظت‌های پایین الکترولیت‌های ضعیف «خوب رفتار»، درجه تفکیک الکترولیت ضعیف با ریشه مربع معکوس غلظت متناسب می‌شود.

الکترولیت های ضعیف معمولی اسیدهای و بازهای ضعیف هستند . غلظت یون ها در محلول یک الکترولیت ضعیف کمتر از غلظت خود الکترولیت است. برای اسیدها و بازها، غلظت ها را می توان زمانی محاسبه کرد که مقدار یا مقادیر ثابت تفکیک اسید مشخص باشد.

برای یک اسید مونوپروتیک ، HA، با رعایت قانون ریشه مربع معکوس، با ثابت تفکیک Ka یک عبارت صریح برای رسانایی به عنوان تابعی از غلظت، c ، که به عنوان قانون رقت استوالد به دست می‌آید.

1 Λ متر = 1 Λ متر 0 + Λ متر ج ک آ ( Λ متر 0 ) 2 display \ displaystyle {\ frac {1} {\ Lambda _ {\ mathrm {m}}}} = {\ frac {1} {\ Lambda _ {\ mathrm {m} {{0}}} + fra \ frac چپ \ Lambda _ {\ mathrm {m}} c} {K _ {\ mathrm {a} چپ \ چپ (\ Lambda _ {\ mathrm {m} ^ {0} \ راست) ^ {2}

حلال‌های مختلف تفکیک یکسانی را نشان می‌دهند اگر نسبت گذردهی نسبی برابر با نسبت ریشه‌های مکعبی غلظت الکترولیت‌ها باشد (قانون والدن).

غلظت های بالاتر

هم قانون کولراوش و هم معادله دبای-هوکل-آنساگر با افزایش غلظت الکترولیت از مقدار معینی شکسته می شوند. دلیل این امر این است که با افزایش غلظت، میانگین فاصله بین کاتیون و آنیون کاهش می یابد، به طوری که برهمکنش بین یون های نزدیک بیشتر می شود. اینکه آیا این ارتباط یونی ، موضوع بحث برانگیزی است. با این حال، اغلب فرض شده است که کاتیون و آنیون برهم کنش می کنند تا یک جفت یونی . بنابراین، یک ثابت “اتصال یونی” K را می توان برای تعادل ارتباط بین یون های A + و B – :

A + + B – ⇌ A + B –  با   K = [A + B − ] / [A + ] [B − ]

دیویس نتایج چنین محاسباتی را با جزئیات زیاد توصیف می‌کند، اما بیان می‌کند که K نباید لزوماً به عنوان یک ثابت تعادل ، بلکه گنجاندن یک اصطلاح “یونی-همبستگی” در گسترش دامنه توافق خوب بین نظریه مفید است. و داده های رسانایی تجربی [14] تلاش های مختلفی برای گسترش درمان Onsager به محلول های متمرکزتر انجام شده است. [15]

شده است که وجود حداقل رسانایی در حلال هایی که دارای گذردهی نسبی زیر 60 هستند، موضوعی بحث برانگیز از نظر تفسیر است. Fuoss و Kraus پیشنهاد کردند که ناشی از تشکیل سه قلوهای یونی است، [16] و این پیشنهاد اخیراً مورد حمایت قرار گرفته است. [17] [18]

پیشرفت‌های دیگری در مورد این موضوع توسط تئودور شیدلوفسکی ، [19] ای. پیتس، [20] آر. ام. فووس، [21] [22] فووس و شدلوفسکی، [23] فووس و اونساگر انجام شده است. [24] [25]

سیستم های حلال مخلوط

رسانایی معادل محدود محلول های مبتنی بر حلال های مخلوط مانند الکل آب بسته به ماهیت الکل حداقل است. برای متانول حداقل 15 مولار درصد آب، [19] [26] [27] و برای اتانول در 6 مولار درصد آب است. [28]

رسانایی در برابر دما

به طور کلی رسانایی یک محلول با افزایش دما افزایش می یابد، زیرا تحرک یون ها افزایش می یابد. برای مقاصد مقایسه، مقادیر مرجع در دمای توافق شده، معمولاً 298 کلوین (≈ 25 درجه سانتیگراد یا 77 درجه فارنهایت) گزارش می شوند، اگرچه گاهی اوقات از 20 درجه سانتیگراد (68 درجه فارنهایت) استفاده می شود. اندازه‌گیری‌های به اصطلاح «جبران» در دمای مناسب انجام می‌شوند، اما مقدار گزارش‌شده یک مقدار محاسبه‌شده از مقدار مورد انتظار رسانایی محلول است، گویی در دمای مرجع اندازه‌گیری شده است. جبران اولیه معمولاً با فرض افزایش خطی رسانایی در مقابل دمای معمولاً 2٪ در هر کلوین انجام می شود. [ نیازمند منبع ] این مقدار به طور گسترده برای اکثر نمک ها در دمای اتاق قابل استفاده است. تعیین ضریب دمایی دقیق برای یک راه حل خاص ساده است و ابزارها معمولاً قادر به اعمال ضریب مشتق شده (یعنی غیر از 2٪) هستند.

اندازه گیری هدایت σ {\displaystyle \sigma } در مقابل دما می توان برای تعیین انرژی فعال سازی استفاده E آ {\displaystyle E_{A}} با استفاده از معادله آرنیوس : [29]

σ = σ 0 ه – E آ / آر تی {\displaystyle \sigma =\sigma _{0}e^{-E_{a}/RT}}

جایی که σ 0 {\displaystyle \sigma _{0}} پیش فاکتور نمایی، R ثابت گاز ، و T دمای مطلق بر حسب کلوین است.

اثر ایزوتوپی حلال

تغییر در رسانایی به دلیل اثر ایزوتوپی برای الکترولیت های دوتره شده قابل توجه است. [30]

برنامه های کاربردی

علیرغم دشواری تفسیر نظری، رسانایی اندازه گیری شده نشانگر خوبی برای وجود یا عدم وجود یون های رسانا در محلول است و اندازه گیری ها به طور گسترده در بسیاری از صنایع استفاده می شود. [31] برای مثال، اندازه‌گیری‌های رسانایی برای نظارت بر کیفیت در منابع آب عمومی، در بیمارستان‌ها، در آب دیگ بخار و صنایعی که به کیفیت آب مانند آبجوسازی وابسته هستند، استفاده می‌شود. این نوع اندازه گیری مختص یون نیست. مشخص باشد، گاهی اوقات می توان از آن برای تعیین مقدار کل جامدات محلول اگر ترکیب محلول و رفتار رسانایی آن [1] اندازه‌گیری‌های رسانایی که برای تعیین خلوص آب انجام می‌شوند به آلاینده‌های غیر رسانا پاسخ نمی‌دهند (بسیاری از ترکیبات آلی در این دسته قرار می‌گیرند)، بنابراین بسته به کاربرد ممکن است آزمایش‌های خلوص اضافی مورد نیاز باشد.

کاربردهای اندازه گیری TDS به استفاده صنعتی محدود نمی شود. بسیاری از مردم از TDS به عنوان شاخص خلوص آب آشامیدنی خود استفاده می کنند. علاوه بر این، علاقه مندان به آکواریوم به TDS توجه دارند، هم برای آکواریوم های آب شیرین و هم برای آب شور. بسیاری از ماهی ها و بی مهرگان به پارامترهای بسیار باریکی برای مواد جامد محلول نیاز دارند. به خصوص برای پرورش موفقیت آمیز برخی از بی مهرگان که معمولاً در آکواریوم های آب شیرین نگهداری می شوند – حلزون ها و میگوها عمدتاً – آب شور با TDS بالاتر، به ویژه شوری بالاتر، آب مورد نیاز است. در حالی که بزرگسالان یک گونه خاص ممکن است در آب های شیرین رشد کنند، این همیشه برای جوانان صادق نیست و برخی از گونه ها اصلاً در آب های غیر شور زاد و ولد نمی کنند.

گاهی اوقات، اندازه‌گیری‌های هدایت با روش‌های دیگر برای افزایش حساسیت تشخیص انواع خاصی از یون‌ها مرتبط می‌شوند. به عنوان مثال، در فناوری آب دیگ بخار، دمش دیگ به طور مداوم برای “رسانایی کاتیونی” کنترل می شود، که رسانایی آب پس از عبور از یک رزین تبادل کاتیونی است. این یک روش حساس برای نظارت بر ناخالصی‌های آنیونی در آب دیگ در حضور کاتیون‌های اضافی (آنهایی که عامل قلیایی‌کننده معمولاً برای تصفیه آب استفاده می‌شوند) است. حساسیت این روش متکی بر تحرک بالای H + در مقایسه با تحرک سایر کاتیون ها یا آنیون ها است. فراتر از رسانایی کاتیونی، ابزارهای تحلیلی طراحی شده برای اندازه گیری رسانایی که در آن رسانایی پس از حذف دی اکسید کربن محلول از نمونه، از طریق جوشاندن مجدد یا گاززدایی دینامیکی اندازه گیری می شود.

آشکارسازهای رسانایی معمولاً با کروماتوگرافی یونی استفاده می شوند . [32]

همچنین مشاهده کنید

  • رابطه انیشتین (نظریه جنبشی)
  • معادله متولد شده
  • اثر دبای – فالکنهاگن
  • قانون رقیق سازی
  • شماره انتقال یون
  • جو یونی
  • اثر وین
  • تیتراسیون هدایت سنجی – روش هایی برای تعیین نقطه هم ارزی

منابع

  • گری، جیمز آر (2004). “آنالایزرهای رسانایی و کاربرد آنها” . در پایین، RD. Lehr, JH (ویرایش‌ها). کتاب ابزار دقیق و تحلیل محیطی . وایلی. صص 491-510. شابک  978-0-471-46354-2 . بازیابی شده در 10 مه 2009 .
  • “رسانایی آب” . لنتک . بازبینی شده در 5 ژانویه 2013 .
  • بوکریس، جی. اوم. ردی، AKN؛ Gamboa-Aldeco، M. (1998). الکتروشیمی مدرن (ویرایش دوم). اسپرینگر. شابک  0-306-45555-2 . بازیابی شده در 10 مه 2009 .
  • Marija Bešter-Rogač و Dušan Habe، “پیشرفت های مدرن در اندازه گیری های هدایت الکتریکی راه حل ها”، Acta Chim. اسلوو. 2006، 53، 391-395 (pdf)
  • بویز، دبلیو (2002). کتاب مرجع ابزار دقیق (ویرایش سوم). باترورث-هاینمن. شابک  0-7506-7123-8 . بازیابی شده در 10 مه 2009 .
  • خاکستری، ص 495
  • دوپلهامر، نیکولاس؛ پلنز، نیک؛ مارتنز، یوهان؛ Kirschhock، کریستین EA; یاکوبی، برنهارد؛ رایشل، اروین کی. (27 اکتبر 2020). “طیف‌سنجی امپدانس الکترود متحرک برای اندازه‌گیری دقیق رسانایی محیط‌های یونی خورنده” . ACS سنسورهای 5 (11): 3392-3397. doi : 10.1021/acssensors.0c01465 . PMC  7706010 . PMID  33107724 .
  • قوش، آرون ک. (2013). مقدمه ای بر اندازه گیری ها و ابزار دقیق (ویرایش چهارم، ویرایش اقتصاد شرق). دهلی: PH Learning. شابک  978-81-203-4625-3 . OCLC  900392417 .
  • “راهنمای سفارش رسانایی” (PDF) . EXW Foxboro. 3 اکتبر 1999. بایگانی شده از نسخه اصلی (PDF) در 7 سپتامبر 2012 . بازبینی شده در 5 ژانویه 2013 .
  • “ASTM D1125 – 95 (2005) روش های تست استاندارد برای رسانایی الکتریکی و مقاومت آب” . بازیابی شده در 12 مه 2009 .
  • آدامسون، آرتور دبلیو (1973). کتاب درسی شیمی فیزیک . لندن: Academic Press inc. پ. 512.
  • بشتر روگاچ، ام. تومشیچ، م. بارتل، جی. نویدر، آر. Apelblat, A. (1 ژانویه 2002). “مطالعات رسانایی محلول های آبی رقیق اسید اگزالیک و اگزالات های خنثی سدیم، پتاسیم، سزیم و آمونیوم از 5 تا 35 درجه سانتی گراد” . مجله شیمی محلول . 31 (1): 1-18. doi : 10.1023/A:1014805417286 . ISSN  1572-8927 . S2CID  92641871 .
  • رایت، MR (2007). مقدمه ای بر محلول های الکترولیت آبی . وایلی. شابک  978-0-470-84293-5 .
  • دیویس، سی دبلیو (1962). انجمن یون . لندن: باترورث.
  • میوشی، ک. (1973). “مقایسه معادلات رسانایی Fuoss-Onsager، Fuoss-Hsia و Pitts با داده های پرکلرات Bis(2،9-dimethyl-1،10-phenanthroline)cu(I)” . گاو نر شیمی. Soc. Jpn . 46 (2): 426-430. doi : 10.1246/bcsj.46.426 .
  • Fuoss, RM; کراوس، کالیفرنیا (1935). “ویژگی های محلول های الکترولیتی. XV. خواص ترمودینامیکی الکترولیت های بسیار ضعیف”. مربا. شیمی. Soc. 57 : 1-4. doi : 10.1021/ja01304a001 .
  • وینگارتنر، اچ. ویس، VC; شروئر، دبلیو (2000). “ارتباط یونی و حداقل رسانایی الکتریکی در تئوری های دبای-هوکل سیال یونی کره سخت”. جی. شیمی. فیزیک . 113 (2): 762–. Bibcode : 2000JChPh.113..762W . doi : 10.1063/1.481822 .
  • شروئر، دبلیو. Weingärtner, H. (2004). “ساختار و بحرانی سیالات یونی” (PDF) . Pure Appl. شیمی . 76 (1): 19-27. doi : 10.1351/pac200476010019 . S2CID  39716065 .
  • شدلوفسکی، تئودور (1932). “رسانایی الکترولیتی برخی از الکترولیت های تک ظرفیتی در آب در دمای 25 درجه”. مجله انجمن شیمی آمریکا . انجمن شیمی آمریکا (ACS). 54 (4): 1411-1428. doi : 10.1021/ja01343a020 . ISSN  0002-7863 .
  • پیتس، ای. کولسون، چارلز آلفرد (1953). “توسعه ای از تئوری هدایت و ویسکوزیته محلول های الکترولیت”. Proc. روی. سوسیال _ A217 (1128): 43. Bibcode : 1953RSPSA.217…43P . doi : 10.1098/rspa.1953.0045 . S2CID  123363978 .
  • Fuoss, Raymond M. (1958). “رسانایی یونوفورها”. مجله انجمن شیمی آمریکا . انجمن شیمی آمریکا (ACS). 80 (12): 3163. doi : 10.1021/ja01545a064 . ISSN  0002-7863 .
  • Fuoss, Raymond M. (1959). “رسانایی محلول های رقیق 1-1 الکترولیت1”. مجله انجمن شیمی آمریکا . انجمن شیمی آمریکا (ACS). 81 (11): 2659-2662. doi : 10.1021/ja01520a016 . ISSN  0002-7863 .
  • فووس، ریموند ام. شدلوفسکی، تئودور. (1949). “برون یابی داده های رسانایی برای الکترولیت های ضعیف”. مجله انجمن شیمی آمریکا . انجمن شیمی آمریکا (ACS). 71 (4): 1496-1498. doi : 10.1021/ja01172a507 . ISSN  0002-7863 .
  • فووس، ریموند ام. اونساگر، لارس (1964). “رسانایی الکترولیت های متقارن.1aIV. اصطلاحات هیدرودینامیکی و اسمزی در زمینه آرامش”. مجله شیمی فیزیک . انجمن شیمی آمریکا (ACS). 68 (1): 1-8. doi : 10.1021/j100783a001 . ISSN  0022-3654 .
  • فووس، ریموند ام. اونساگر، لارس; اسکینر، جیمز اف (1965). “رسانایی الکترولیت های متقارن. V. معادله رسانایی 1،2”. مجله شیمی فیزیک . انجمن شیمی آمریکا (ACS). 69 (8): 2581-2594. doi : 10.1021/j100892a017 . ISSN  0022-3654 .
  • شدلوفسکی، تئودور؛ کی، رابرت ال (1956). “ثابت یونیزاسیون اسید استیک در مخلوط آب- متانول در 25 درجه از اندازه گیری های رسانایی”. مجله شیمی فیزیک . انجمن شیمی آمریکا (ACS). 60 (2): 151-155. doi : 10.1021/j150536a003 . ISSN  0022-3654 .
  • استرلو، اچ. (1960). “اثر آب بر رسانایی معادل HCl در متانول”. مجله شیمی فیزیک . والتر دو گروتر جیامبیایچ. 24 (3-4): 240-248. doi : 10.1524/zpch.1960.24.3_4.240 . ISSN  0942-9352 .
  • بزمن، ایروینگ آی. ورهوک، فرانک اچ (1945). “رسانایی کلرید هیدروژن و کلرید آمونیوم در مخلوط اتانول-آب”. مجله انجمن شیمی آمریکا . انجمن شیمی آمریکا (ACS). 67 (8): 1330–1334. doi : 10.1021/ja01224a035 . ISSN  0002-7863 .
  • پتروفسکی، مت؛ فرچ، راجر (30 آوریل 2009). “وابستگی انتقال یون به دما: معادله آرنیوس جبران شده” . مجله شیمی فیزیک ب . 113 (17): 5996-6000. doi : 10.1021/jp810095g . ISSN  1520-6106 . PMID  19338318 .
  • بیسواس، رنجیت (1997). “رسانایی یونی محدود کننده یون های متقارن و صلب در محلول های آبی: وابستگی به دما و اثرات ایزوتوپ حلال”. مجله انجمن شیمی آمریکا . 119 (25): 5946-5953. doi : 10.1021/ja970118o .
  • “اندازه گیری هدایت الکترولیتی، تئوری و عمل” (PDF) . Aquarius Technologies Pty Ltd. بایگانی شده از نسخه اصلی (PDF) در 12 سپتامبر 2009.

” آشکارسازهای کروماتوگرافی تبادل یونی ” . بایگانی شده از نسخه اصلی در 20 اوت 2009 . بازیابی شده در 17 مه 2009 .

هدایت یونی (حالت جامد)

پرش به پیمایش پرش به جستجو

یک هادی پروتون ساکن میدان الکتریکی .

رسانایی یونی (که با λ ) معیاری از تمایل یک ماده به سمت هدایت یونی است. هدایت یونی حرکت یون ها است. این پدیده در جامدات و محلول ها مشاهده می شود. هدایت یونی یکی از مکانیسم های جریان است.

در جامدات کریستالی

در بیشتر جامدات، یون‌ها به‌طور صلب موقعیت‌های ثابتی را اشغال می‌کنند که به‌شدت توسط اتم‌ها یا یون‌های همسایه در آغوش گرفته می‌شوند. در برخی از جامدات، یون‌های انتخاب شده بسیار متحرک هستند و امکان هدایت یونی را فراهم می‌کنند. تحرک با دما افزایش می یابد. موادی که این ویژگی را نشان می دهند در باتری ها استفاده می شوند. یک جامد رسانای یونی شناخته شده β”-آلومینا (“BASE”)، شکلی از اکسید آلومینیوم است که کانال هایی دارد که کاتیون های سدیم می توانند از طریق آنها عبور کنند. هنگامی که این سرامیک با یک یون مانند Na + می شود، به اصطلاح به عنوان رسانای یون سریع . BASE به عنوان یک غشاء در چندین نوع نمک مذاب سلول الکتروشیمیایی .

در عینک

هدایت یونی در جامدات بی نظم مانند شیشه ها، پلیمرها، نانوکامپوزیت ها، کریستال های معیوب و سایر جامدات بی نظم نقش مهمی در فناوری ایفا می کند.

تاریخچه

هدایت یونی در جامدات از ابتدای قرن نوزدهم موضوع مورد توجه بوده است. مایکل فارادی در سال 1839 اعلام کرد که قوانین الکترولیز در جامدات یونی مانند II) ( PbF 2 ) و سولفید نقره ( Ag 2 S ). جامد یدید نقره ( AgI دارای رسانایی یونی فوق‌العاده بالایی در دماهای بالاتر از 147 درجه سانتیگراد است، AgI به فازی تبدیل می‌شود که دارای رسانایی یونی ~1-1cm- 1 است. این فاز دمای بالا AgI نمونه ای از یک هادی . ساختار بی نظم این جامد به + یون های دارنده رکورد کنونی برای هدایت یونی، ماده مرتبط Ag 2 HgI 4 است. [4] β”-آلومینا در شرکت فورد موتور در جستجوی یک وسیله ذخیره سازی برای وسایل نقلیه الکتریکی در حالی که در حال توسعه باتری سدیم-گوگرد بود یافت.

همچنین مشاهده کنید

  • انرژی شبکه
  • هادی یونی سریع
  • NASICON

منابع

  • ریچارد تورتون. (2000). فیزیک جامدات. نیویورک: انتشارات دانشگاه آکسفورد. شابک  0-19-850352-0 .
  • لو، Xiaochuan; شیا، گوانگوانگ؛ لمون، جان پی. یانگ، ژنگو (2010). “مواد پیشرفته برای باتری های آلومینا سدیم-بتا: وضعیت، چالش ها و دیدگاه ها”. مجله منابع برق . 195 (9): 2431-2442. Bibcode : 2010JPS…195.2431L . doi : 10.1016/j.jpowsour.2009.11.120 .
  • Dyre، Jeppe C; ماس، فیلیپ؛ رولینگ، برنهارد؛ ساید باتم، دیوید ال (2009). “سوالات اساسی مربوط به هدایت یونی در جامدات بی نظم” . گزارش پیشرفت در فیزیک . 72 (4): 046501. arXiv : 0803.2107 . Bibcode : 2009RPPh…72d6501D . doi : 10.1088/0034-4885/72/4/046501 . ISSN  0034-4885 . S2CID  53075476 .

گرین وود، نورمن ن . ارنشاو، آلن (1997). شیمی عناصر (ویرایش دوم). باترورث-هاینمن . پ. 800. شابک  978-0-08-037941-8 .

رسانایی

رسانایی چیست و چرا اهمیت دارد؟

رسانایی اندازه گیری توانایی آب برای عبور جریان الکتریکی است. رسانایی در آب تحت تأثیر وجود مواد جامد غیر آلی محلول مانند کلرید، نیترات، سولفات، و آنیون‌های فسفات (یون‌های حامل بار منفی) یا کاتیون‌های سدیم، منیزیم، کلسیم، آهن و آلومینیوم (یون‌های حامل بار مثبت) است. ). ترکیبات آلی مانند روغن، فنل، الکل و شکر جریان الکتریکی را به خوبی هدایت نمی کنند و بنابراین در آب رسانایی کمی دارند. رسانایی نیز تحت تأثیر دما قرار می گیرد: هرچه آب گرمتر باشد رسانایی بالاتری دارد. به همین دلیل، رسانایی به عنوان رسانایی در دمای 25 درجه سانتیگراد (25 درجه سانتیگراد) گزارش می شود.

رسانایی در نهرها و رودخانه ها عمدتاً تحت تأثیر زمین شناسی منطقه ای است که آب از طریق آن جریان دارد. جریان هایی که از میان مناطقی با سنگ بستر گرانیتی عبور می کنند، رسانایی کمتری دارند زیرا گرانیت از مواد بی اثر تری تشکیل شده است که هنگام شستشو در آب یونیزه نمی شوند (به اجزای یونی حل می شوند). از سوی دیگر، نهرهایی که از مناطقی با خاک رسی عبور می کنند، به دلیل وجود موادی که هنگام شستن در آب یونیزه می شوند، رسانایی بالاتری دارند. جریان آب زیرزمینی بسته به سنگ بستری که از آن عبور می کند می تواند اثرات یکسانی داشته باشد.

تخلیه به جریان می تواند رسانایی را بسته به ترکیب آنها تغییر دهد. خرابی سیستم فاضلاب رسانایی را به دلیل وجود کلرید، فسفات و نیترات افزایش می دهد. نشت نفت رسانایی را کاهش می دهد.

واحد اصلی اندازه گیری رسانایی mho یا زیمنس است. رسانایی بر حسب میکرومس بر سانتیمتر (µmhos/cm) یا میکروزیمنس بر سانتی‌متر (µs/cm) اندازه‌گیری می‌شود. رسانایی آب مقطر در محدوده 0.5 تا 3 میکرومتر بر سانتی متر است. رسانایی رودخانه ها در ایالات متحده به طور کلی بین 50 تا 1500 میکرومتر بر سانتی متر است. مطالعات آب‌های شیرین داخلی نشان می‌دهد که جریان‌هایی که از ماهیگیری ترکیبی خوب حمایت می‌کنند، محدوده‌ای بین 150 تا 500 µhos/cm دارند. رسانایی خارج از این محدوده می تواند نشان دهد که آب برای گونه های خاصی از ماهی ها یا بی مهرگان بزرگ مناسب نیست. آب های صنعتی می توانند تا 10000 میکرومتر بر سانتی متر باشد.

ملاحظات نمونه برداری و تجهیزات

رسانایی به عنوان یک معیار کلی برای کیفیت آب رودخانه مفید است. هر جریان دارای محدوده نسبتاً ثابتی از رسانایی است که پس از ایجاد، می تواند به عنوان یک خط پایه برای مقایسه با اندازه گیری های رسانایی معمولی استفاده شود. تغییرات قابل توجه در رسانایی می تواند نشانگر این باشد که تخلیه یا منبع دیگری از آلودگی وارد یک جریان شده است.

رسانایی با یک پروب و یک متر اندازه گیری می شود. ولتاژ بین دو الکترود در یک پروب غوطه ور در آب نمونه اعمال می شود. افت ولتاژ ناشی از مقاومت آب برای محاسبه رسانایی بر سانتی متر استفاده می شود. متر اندازه گیری کاوشگر را به micromhos بر سانتی متر تبدیل می کند و نتیجه را برای کاربر نمایش می دهد. توجه: برخی از رسانایی سنج ها را می توان برای آزمایش کل جامدات محلول و شوری نیز استفاده کرد. غلظت کل مواد جامد محلول بر حسب میلی گرم در لیتر (میلی گرم در لیتر) را نیز می توان با ضرب نتیجه رسانایی در ضریبی بین 0.55 تا 0.9 محاسبه کرد که به صورت تجربی تعیین می شود (به روش های استاندارد #2510، APHA 1992 مراجعه کنید).

رسانایی متر مناسب حدود 350 دلار هزینه دارد. مترها در این بازه قیمتی باید دما را اندازه گیری کنند و به طور خودکار دما را در قرائت رسانایی جبران کنند. رسانایی را می توان در مزرعه یا آزمایشگاه اندازه گیری کرد. در بیشتر موارد، احتمالاً بهتر است نمونه ها در میدان جمع آوری شده و برای آزمایش به آزمایشگاه برده شوند. به این ترتیب چندین تیم از داوطلبان می توانند نمونه ها را به طور همزمان جمع آوری کنند. اگر آزمایش در میدان مهم است، مترهایی که برای استفاده در میدان طراحی شده اند را می توان با همان هزینه ای که در بالا ذکر شد به دست آورد.

اگر نمونه‌ها برای اندازه‌گیری بعدی در مزرعه جمع‌آوری می‌شوند، بطری نمونه باید یک بطری شیشه‌ای یا پلی اتیلن باشد که در مواد شوینده بدون فسفات شسته شده و با آب لوله کشی و مقطر کاملاً شسته شده باشد. ممکن است از کیسه های Whirl-pak® آماده شده در کارخانه استفاده شود.

نحوه نمونه برداری

روش های جمع آوری نمونه ها و تجزیه و تحلیل رسانایی شامل وظایف زیر است:

وظیفه 1 ظروف نمونه را آماده کنید

اگر برای نمونه برداری از کیسه های یکبار مصرف Whirl-pak® مهر و موم شده در کارخانه استفاده شود، نیازی به آماده سازی نیست. ظروف نمونه استفاده مجدد (و تمام ظروف شیشه ای مورد استفاده در این روش) باید قبل از اولین اجرا و بعد از هر نمونه برداری با پیروی از روش A همانطور که در روش A در جدول 1 در فصل 5 – شرایط کیفیت آب .

وظیفه 2 قبل از عزیمت به محل نمونه برداری آماده شوید

مراجعه کنید بخش 2.3 – ملاحظات ایمنی برای جزئیات در مورد تأیید تاریخ و زمان نمونه برداری، ملاحظات ایمنی، بررسی منابع، و بررسی آب و هوا و جهت ها، علاوه بر تجهیزات و پوشاک نمونه‌برداری استاندارد، هنگام نمونه‌برداری برای هدایت، تجهیزات زیر را نیز شامل می‌شود:

  • رسانایی متر و پروب (در صورت آزمایش رسانایی در میدان)
  • استاندارد رسانایی مناسب برای محدوده معمولی جریان
  • برگه داده برای رسانایی برای ثبت نتایج

مطمئن شوید که به کسی اطلاع دهید که کجا می روید و چه زمانی می خواهید برگردید.

وظیفه 3 جمع آوری نمونه (اگر نمونه ها در آزمایشگاه آزمایش شوند)

به وظیفه 2 در فصل 5 – شرایط کیفیت آب برای جزئیات نحوه جمع‌آوری نمونه‌های آب با استفاده از بطری‌های درپوش پیچی یا کیسه‌های Whirl-pak®،

وظیفه 4 تجزیه و تحلیل نمونه (میدان یا آزمایشگاه)

روش زیر برای استفاده میدانی یا آزمایشگاهی از رسانایی سنج اعمال می شود.

  1. رسانایی سنج را طبق دستورالعمل سازنده برای استفاده آماده کنید.
  2. از محلول استاندارد رسانایی (معمولاً کلرید پتاسیم یا کلرید سدیم) برای کالیبره کردن متر برای محدوده ای که اندازه گیری می کنید استفاده کنید. دستورالعمل های سازنده باید روش های آماده سازی محلول استاندارد را تشریح کند.
  3. پروب را با آب مقطر یا دیونیزه بشویید.
  4. محدوده مناسب را انتخاب کنید که از بالاترین محدوده شروع می شود و پایین می آید. رسانایی نمونه آب را بخوانید. اگر قرائت در 10 درصد پایین‌تر محدوده است، به محدوده پایین‌تر بعدی بروید. اگر رسانایی نمونه بیشتر از محدوده ابزار باشد، می توانید نمونه را رقیق کنید. حتماً رقیق‌سازی را طبق دستورالعمل سازنده انجام دهید زیرا ممکن است رقیق‌سازی رابطه خطی ساده‌ای با رسانایی نداشته باشد.
  5. پروب را با آب مقطر یا دیونیزه بشویید و مرحله 4 را تا پایان تکرار کنید.

وظیفه 5 نمونه ها و برگه های داده های میدانی را به آزمایشگاه/نقطه رها کردن برگردانید.

نمونه هایی که برای تجزیه و تحلیل رسانایی به آزمایشگاه فرستاده می شوند باید ظرف 28 روز پس از جمع آوری آزمایش شوند. نمونه ها را روی یخ یا در یخچال نگهداری کنید.

منابع

APHA. 1992. روشهای استاندارد برای بررسی آب و فاضلاب. 18 چاپ _ انجمن بهداشت عمومی آمریکا، واشنگتن دی سی.

شرکت هاچ. 1371. راهنمای تجزیه و تحلیل آب هاچ. ویرایش دوم لاولند، کو.

دیده بان رودخانه هدواتر می سی سی پی. 1991. رویه های کیفیت آب. هیئت مدیره می سی سی پی مارس.

 

شاخص ها: رسانایی

رسانایی چیست؟

رسانایی اندازه گیری توانایی آب برای عبور جریان الکتریکی است. از آنجایی که نمک های محلول و سایر مواد شیمیایی معدنی، جریان الکتریکی را هدایت می کنند، با افزایش شوری رسانایی افزایش می یابد. ترکیبات آلی مانند روغن جریان الکتریکی را به خوبی هدایت نمی کنند و بنابراین در آب رسانایی کمی دارند. رسانایی نیز تحت تأثیر دما قرار می گیرد: هرچه آب گرمتر باشد رسانایی بالاتری دارد.

چرا ارزیابی رسانایی مهم است؟

رسانایی به عنوان معیار کلی کیفیت آب مفید است. هر بدنه آبی دارای یک محدوده نسبتاً ثابت از رسانایی است که پس از ایجاد، می‌تواند به عنوان یک خط پایه برای مقایسه با اندازه‌گیری‌های هدایت معمولی استفاده شود. تغییرات قابل توجهی در رسانایی می تواند نشانگر این باشد که تخلیه یا منبع دیگری از آلودگی وارد منابع آبی شده است.

رسانایی می تواند در مورد وضعیت آب به ما بگوید؟

تغییرات قابل توجه (معمولاً افزایش) در رسانایی ممکن است نشان دهنده این باشد که یک تخلیه یا منبع اختلال دیگری باعث کاهش وضعیت نسبی یا سلامت بدنه آبی و موجودات زنده مرتبط با آن شده است. به طور کلی، اختلالات انسانی تمایل به افزایش مقدار مواد جامد محلول وارد آب دارد که منجر به افزایش رسانایی می شود. اجسام آبی با رسانایی بالا ممکن است سایر شاخص های مختل یا تغییر یافته را نیز داشته باشند.

 

 

 

دیدگاهتان را بنویسید

نشانی ایمیل شما منتشر نخواهد شد. بخش‌های موردنیاز علامت‌گذاری شده‌اند *