ما هو قانون القصور الذاتي؟

القصور الذاتي هو فكرة أن الجسم يستمر في حركته الحالية حتى تؤدي القوة إلى تغيير سرعته أو اتجاهه. يُفهم المصطلح بشكل صحيح على أنه اختصار لـ “مبدأ القصور الذاتي” الذي شرحه نيوتن في قانونه الأول للحركة.

وبعد تعريفات أخرى يقول نيوتن في قانونه الأول للحركة:

القانون 1. يظل كل جسم في حالة السكون أو الحركة المنتظمة في خط مستقيم، ما لم تضطر إلى تغيير تلك الحالة بواسطة القوى المؤثرة عليه.

كلمة “المثابرة” هي ترجمة مباشرة من الكلمة اللاتينية نيوتن. توجد مصطلحات أخرى أقل شيوعًا مثل “الاستمرار” أو “البقاء” بشكل شائع في الكتب المدرسية الحديثة. الاستخدام الحديث لبعض التعديلات على ميكانيكا نيوتن الأصلية (كما تم التعبير عنها في كتاب المبادئ) جاء من أويلر ودالمبرت وغيرهما من الديكارتيين.

مصطلح القصور الذاتي مشتق من الكلمة اللاتينية iners والتي تعني الخمول أو الكسل. قد يشير مصطلح القصور الذاتي أيضًا إلى مقاومة أي جسم مادي للتغير في سرعته. وهذا يشمل التغيرات في السرعة أو اتجاه الحركة. أحد جوانب هذه الخاصية هو ميل الأجسام للتحرك في خط مستقيم وبسرعة ثابتة عندما لا تؤثر عليها أي قوى.

يعد القصور الذاتي أحد المظاهر الأساسية للكتلة، وهي إحدى الخصائص الكمية للأنظمة الفيزيائية.

في كتابه تاريخ الفلسفة الطبيعية، مبادئ الرياضيات، عرّف إسحاق نيوتن القصور الذاتي بأنه قوة:

التعريف الثالث. إن القوة الفطرية للمادة هي قوة المقاومة التي يحاول من خلالها أي جسم، بقدر ما يقع فيه، أن يحافظ على حالته الحالية، سواء كان في حالة سكون أو يتحرك بشكل منتظم للأمام في خط مستقيم.

مبدأ القصور الذاتي هو أحد المبادئ الأساسية في الفيزياء الكلاسيكية. ولا يزال يستخدم حتى اليوم لوصف حركة الأشياء وكيفية تأثير القوى المطبقة عليها.

تاريخ وتطور المفهوم

الفهم الأساسي للحركة بالقصور الذاتي

جون ه. يشير لينهارد إلى أن موزي – استنادًا إلى نص صيني من فترة الممالك المتحاربة (221-475 قبل الميلاد) – قدم أول وصف للقصور الذاتي. في أوروبا قبل عصر النهضة، كانت نظرية الحركة الشائعة في الفلسفة الغربية هي نظرية أرسطو (335 قبل الميلاد إلى 322 قبل الميلاد). على سطح الأرض، غالبًا ما يتم إخفاء خاصية القصور الذاتي للأجسام المادية عن طريق الجاذبية وتأثيرات الاحتكاك ومقاومة الهواء، وكلاهما يميل إلى إبطاء الأجسام المتحركة (عادةً إلى نقطة السكون). وهذا ما دفع الفيلسوف أرسطو إلى الاعتقاد بأن الأجسام تتحرك فقط عندما يتم تطبيق قوة عليها. قال أرسطو أن جميع الأجسام المتحركة (على الأرض) ستستقر في نهاية المطاف ما لم تحافظ عليها قوة خارجية (قوة) على الحركة. أوضح أرسطو الحركة المستمرة للمقذوفات بعد انفصالها عن أجهزة العرض الخاصة بها كعمل (لا يحتاج إلى شرح) للبيئة المحيطة التي استمرت في تحريك المقذوف.

على الرغم من قبوله العام، فقد كان مفهوم أرسطو للحركة محل نزاع في مناسبات عديدة من قبل فلاسفة بارزين على مدار ما يقرب من ألفي عام. على سبيل المثال، أكد لوكريتيوس (ربما بعد أبيقور) أن “الحالة الافتراضية” للمادة هي الحركة، وليس الركود. في القرن السادس، انتقد جون فيلوبونوس التناقض بين مناقشة أرسطو للمقذوفات، حيث يدعم الوسط المقذوفات، ومناقشته للفضاء الفارغ، حيث يمنع الوسط الجسم من الحركة. اقترح فيلوبونوس أن الحركة لا يتم الحفاظ عليها من خلال عمل البيئة المحيطة، ولكن من خلال بعض الخصائص المنقولة إلى الجسم عندما يتم تحريكه. على الرغم من أن هذا لم يكن المفهوم الحديث للقصور الذاتي، حيث كان لا يزال هناك حاجة إلى قوة للحفاظ على حركة الجسم، إلا أنه أثبت أنه خطوة أساسية في هذا الاتجاه. وقد عارض ابن رشد والعديد من الفلاسفة المدرسيين الآخرين الذين دعموا أرسطو هذا الرأي بشدة.

في القرن الحادي عشر، ادعى الشاعر الإيراني ابن سينا ​​(أبو سينا) أن المقذوف لن يتوقف في الفراغ ما لم يتم التصرف بناءً عليه.

نظرية التحفيز (ما هو قانون القصور الذاتي) 

في القرن الرابع عشر، رفض جان بوريدان فكرة أن الخاصية التوليدية للحركة، والتي أسماها الدافع، سوف تختفي من تلقاء نفسها. كان موقف بوريدان هو أن الجسم المتحرك يتم احتجازه بواسطة مقاومة الهواء ووزن الجسم الذي يتعارض مع القوة الدافعة له. وذكر بوريدان أيضًا أن الدافع يزداد مع السرعة. وهكذا، كانت فكرته المبكرة عن الدافع مشابهة في كثير من النواحي للمفهوم الحديث للاندفاع. على الرغم من أوجه التشابه الواضحة مع الأفكار الأكثر حداثة حول القصور الذاتي، رأى بوريدان نظريته على أنها مجرد تعديل لفلسفة أرسطو الأساسية، واحتفظ بالعديد من وجهات نظره الأخرى، بما في ذلك الاعتقاد بأنه لا يزال هناك فرق جوهري بين الجسم المتحرك والجسم في حالة حركة. راحة هناك. . يعتقد بوريدان أيضًا أن النبضات لا يمكن أن تكون خطية فحسب، بل دائرية أيضًا، مما يتسبب في تحرك الأجسام (مثل الأجرام السماوية) في دائرة. وقد تبع نظرية بوريدان تلميذه ألبرت الساكسوني (1316-1390) وآلات أكسفورد الحاسبة. أجرى العديد من التجارب التي أدت إلى تقويض النموذج الأرسطي. وقد تم شرح عملهم بدوره بواسطة نيكول أوريسمي، التي كانت رائدة في ممارسة توضيح قوانين الحركة باستخدام الرسوم البيانية.

قبل وقت قصير من نظرية جاليليو عن القصور الذاتي، قام جيامباتيستا بينيديتي بتعديل النظرية المتنامية للدفعة لتشمل الحركة الخطية وحدها:

“…[كل] جزء من المادة المادية، الذي يتحرك من تلقاء نفسه، عندما يؤثر عليه دافع من أي قوة دافعة خارجية، له ميل طبيعي للتحرك في مسار مستقيم، وليس منحني”.

يستشهد بينيديتي بحركة الحجر في السلسلة كمثال على الحركة الخطية المتأصلة للأجسام، والتي يتم تحفيزها إلى حركة دائرية.

الجمود الكلاسيكي

وفقًا لتشارلز كولستون جيليسبي، فإن القصور الذاتي “كنتيجة فيزيائية هندسية ديكارتية لمسألة الفضاء، جنبًا إلى جنب مع ثبات اللهدخل العلم. كان أول فيزيائي انفصل تمامًا عن النموذج الأرسطي للحركة هو إسحاق بيكمان في عام 1614. تم تقديم مصطلح “القصور الذاتي” لأول مرة بواسطة يوهانس كيبلر في كتابه Epitome Astronomiae Copernicanae (الذي نُشر في ثلاثة مجلدات). 1617 إلى 1621)؛ ومع ذلك، فإن معنى كيبلر للمصطلح (الذي اشتقه من الكلمة اللاتينية التي تعني “الكسل” أو “الكسل”) لم يكن تمامًا نفس تفسيره الحديث. عرّف كيبلر القصور الذاتي فقط من خلال مقاومة الحركة، مرة أخرى على فرضية أن السكون هو حالة طبيعية لا تحتاج إلى تفسير. لم يكن الأمر كذلك حتى الأعمال اللاحقة لجاليليو ونيوتن التي وحدت الراحة والحركة في مبدأ واحد حتى يمكن تطبيق مصطلح “القصور الذاتي” على هذه المفاهيم كما هو اليوم. مبدأ القصور الذاتي، كما صاغه أرسطو لـ “الحركات في الفضاء الفارغ”. [25] وهو يعني أن الجسم الدنيوي يميل إلى مقاومة التغيير في الحركة.

غاليليو، في مواصلة تطوير النموذج الكوبرنيكي (ما هو قانون القصور الذاتي)

لقد أدرك هذه المشكلات المتعلقة بالطبيعة المقبولة للحركة في ذلك الوقت، وبالتالي، تضمن، على الأقل جزئيًا، إعادة صياغة لوصف أرسطو للحركة في الفراغ كمبدأ فيزيائي أساسي:

يستمر الجسم المتحرك على سطح أملس في الاتجاه نفسه بسرعة ثابتة ما لم يتعرض لأي اضطراب.

يكتب جاليليو أن “جميع العوائق الخارجية، أي الجسم الثقيل الموجود على سطح كروي متحد المركز مع الأرض، يحافظ على نفسه في الحالة التي كان عليها؛ على سبيل المثال، إذا كان يتحرك باتجاه الغرب، فإنه سيحافظ على نفسه في هذا الوضع. تلك الحركة.” [27] هذا المفهوم، الذي يطلق عليه “القصور الذاتي الدائري” أو “القصور الذاتي الدائري الأفقي” من قبل مؤرخي العلوم، هو مقدمة لمفهوم نيوتن للقصور الذاتي المستطيل، ولكنه يختلف عنه. [28] [29] بالنسبة لغاليليو، تكون الحركة “أفقية” إذا لم تحرك الجسم المتحرك نحو أو بعيدًا عن مركز الأرض، وبالنسبة له، “على سبيل المثال، سفينة أعطيت ذات مرة قوة دافعة. يتحرك المحيط الهادئ باستمرار حول عالمنا دون توقف. [30] [31] ومن الجدير بالذكر أيضًا أن غاليليو خلص لاحقًا (في عام 1632) إلى أنه بناءً على هذا الافتراض الأولي للقصور الذاتي، كان من المستحيل معرفة الفرق بين جسم متحرك وجسم ثابت دون مرجع خارجي للمقارنة. عليه. ضد

قام بتنقيح وتعديل وتدوين مفاهيم القصور الذاتي في كتابات جاليليو لاحقًا بواسطة إسحاق نيوتن باعتباره أول قانون للحركة (نُشر لأول مرة في كتاب نيوتن Philosophiæ Naturalis Principia Mathematica، 1687):

يستمر أي جسم في حالة السكون أو الحركة المنتظمة في خط مستقيم ما لم يضطر إلى تغيير تلك الحالة بواسطة القوى المؤثرة عليه.

وعلى الرغم من أن نيوتن عرّف هذا المفهوم بشكل جميل في قوانينه للحركة، إلا أنه لم يستخدم في الواقع مصطلح “القصور الذاتي” للإشارة إلى قانونه الأول. في الواقع، اعتبر في الأصل أن هذه الظاهرة ذات الصلة ناجمة عن “القوى الجوهرية” الكامنة في المادة التي تقاوم أي تسارع. وفقًا لهذا الرأي واستعارة من كبلر، أرجع نيوتن مصطلح “القصور الذاتي” إلى “القوة الكامنة في الجسم التي تقاوم التغيرات في الحركة”. ولذلك، عرّف نيوتن “القصور الذاتي” بأنه يعني سبب الظاهرة، وليس الظاهرة نفسها. ومع ذلك، فإن أفكار نيوتن المبكرة حول “القوة الكامنة للمقاومة” كانت في نهاية المطاف إشكالية لأسباب مختلفة، ولذلك لم يعد معظم الفيزيائيين يفكرون بهذه المصطلحات. وبما أنه لا يتم قبول أي آلية بديلة بسهولة، ومن المقبول الآن بشكل عام أنه قد لا تكون هناك آلية نعرفها، فإن مصطلح “القصور الذاتي” يشير ببساطة إلى الظاهرة نفسها وليس إلى أي آلية جوهرية. إذن، أخيرًا، “القصور الذاتي” في الفيزياء الكلاسيكية الحديثة هو اسم لنفس الظاهرة التي وصفها قانون نيوتن الأول للحركة، ويعتبر المفهومان الآن متساويين.

النسبية

بُنيت نظرية ألبرت أينشتاين في النسبية الخاصة، كما وردت في ورقته البحثية عام 1905 بعنوان “حول الديناميكا الكهربائية للأجسام المتحركة”، على فهم الأطر المرجعية بالقصور الذاتي التي طورها غاليليو وهويجنز ونيوتن. في حين أن هذه النظرية الثورية غيرت بشكل كبير معنى العديد من المفاهيم النيوتونية مثل الكتلة والطاقة والمسافة، إلا أن مفهوم أينشتاين للقصور الذاتي ظل في البداية دون تغيير عن المعنى الأصلي لنيوتن. ومع ذلك، أدى هذا إلى وجود قيود متأصلة في النسبية الخاصة: لا يمكن تطبيق مبدأ النسبية إلا على الإطارات المرجعية بالقصور الذاتي. ولمعالجة هذا القيد، طور أينشتاين نظريته في النسبية العامة (“أساسيات النسبية العامة”، 1916)، والتي اقترحت نظرية تتضمن أطر مرجعية غير قصورية (متسارعة).

في النسبية العامة، اكتسب مفهوم الحركة بالقصور الذاتي معنى أوسع. بالنظر إلى النسبية العامة، يتم تعريف الحركة بالقصور الذاتي على أنها أي حركة فيزيائية لا تتأثر بالمصادر الكهربائية أو المغناطيسية أو غيرها، ولكن فقط بكتل الجاذبية. من الناحية المادية، هذا هو بالضبط ما لا يكتشفه مقياس التسارع ثلاثي المحاور، مما يشير إلى أنه يعمل بشكل صحيح، عندما لا يحصل على أي تسارع لائق.

القصور الدوراني

الكمية المرتبطة بالقصور الذاتي هي القصور الذاتي الدوراني (لحظة القصور الذاتي)، وهي خاصية أن الجسم الصلب الدوار يحافظ على حركته الدورانية المنتظمة. يبقى هذا الزخم الزاوي الخارجي دون تغيير ما لم يتم تطبيق عزم الدوران. وهذا ما يسمى الحفاظ على الزخم الزاوي. غالبًا ما يُنظر إلى القصور الذاتي الدوراني على أنه مرتبط بجسم صلب. على سبيل المثال، يستخدم الجيروسكوب هذه الخاصية لمقاومة أي تغيير في محور الدوران.

جزء من سلسلة في
الميكانيكا الكلاسيكية
F = الـ دي.دي.تي (م ت) القانون الثاني للحركة
تاريخ الجدول الزمني الكتب التعليمية

في الفيزياء الكلاسيكية والنسبية الخاصة، الإطار المرجعي بالقصور الذاتي (ويسمى أيضًا الإطار المرجعي بالقصور الذاتي، أو الإطار بالقصور الذاتي، أو الفضاء بالقصور الذاتي، أو الإطار المرجعي الجليلي) هو إطار مرجعي لا يخضع لأي تسارع. إنها الإطار الذي يتحرك فيه جسم مادي معزول – جسم لا تؤثر عليه قوة صافية – بسرعة ثابتة (ربما سرعة صفر)، أو ما يعادل ذلك، الإطار المرجعي الذي ينطبق عليه قانون نيوتن الأول للحركة. في الحركة المستمرة والمستطيلة، تكون جميع الإطارات بالقصور الذاتي لبعضها البعض. بمعنى آخر، سيكتشف مقياس التسارع المتحرك بأي منهما تسارعًا صفرًا.

وقد لوحظ أن الأجرام السماوية البعيدة عن الأجسام الأخرى والتي تكون في حركة موحدة بسبب إشعاع الخلفية الكونية الميكروي، تحافظ على مثل هذه الحركة المنتظمة.

تحويلها إلى قياس في آخر: يمكن إجراء القياسات في إطار القصور الذاتي عن طريق تحويل بسيط، تحويل غاليليو في الفيزياء النيوتونية وتحويل لورنتز في النسبية الخاصة.

في الميكانيكا التحليلية، يمكن تعريف الإطار المرجعي بالقصور الذاتي بأنه إطار مرجعي يصف الزمان والمكان بطريقة متجانسة ومتناحية ومستقلة عن الزمن.

في النسبية العامة

• في أي منطقة صغيرة بما يكفي بحيث يكون انحناء الزمكان وقوى المد والجزر [5] مهملة، يمكن للمرء العثور على مجموعة من إطارات القصور الذاتي التي تصف تلك المنطقة تقريبًا.
• يمكن وصف فيزياء النظام [7] من حيث إطار القصور الذاتي مع عدم وجود أسباب خارجية للنظام المعني، باستثناء التأثير الظاهري الناجم عن ما يسمى بالكتل البعيدة.

في الإطار المرجعي غير القصوري، من وجهة نظر الفيزياء الكلاسيكية والنسبية الخاصة، تختلف التفاعلات بين المكونات الأساسية للعالم المرئي (فيزياء النظام) اعتمادًا على تسارع ذلك الإطار مقارنةً بإطار مرجعي غير قصوري. إطار ذاتي. من وجهة النظر هذه، وبسبب ظاهرة القصور الذاتي، فإن القوى الفيزيائية “العادية” بين جسمين يجب أن تُستكمل بقوى قصورية تبدو عديمة المصدر. [9] [10] من وجهة نظر النظرية النسبية العامة، تُعزى قوى القصور الذاتي الظاهرة (أسباب خارجية تكميلية) إلى الحركة الجيوديسية في الزمكان.

على سبيل المثال، في الفيزياء الكلاسيكية، الكرة التي تسقط نحو الأرض لا تتحرك تمامًا إلى الأسفل لأن الأرض تدور. وهذا يعني أن الإطار المرجعي للمراقب على الأرض ليس بالقصور الذاتي. وبالتالي، يجب على الفيزياء أن تأخذ في الاعتبار تأثير كوريوليس – وهي قوة ظاهرة – للتنبؤ بالحركة الأفقية الصغيرة المقابلة. مثال آخر للقوة الواضحة التي تظهر في الإطارات المرجعية الدوارة يرتبط بتأثير الطرد المركزي، قوة الطرد المركزي.

مجموعة من الإطارات حيث قوانين الفيزياء بسيطة

لا يمكن وصف حركة جسم ما إلا بالنسبة لشيء آخر، مثل كائنات أخرى، أو مراقبين، أو مجموعة من إحداثيات الزمكان. وتسمى هذه الإطارات المرجعية. إذا تم اختيار الإحداثيات بشكل سيء، فقد تبدو قواعد الحركة أكثر تعقيدًا من اللازم. على سبيل المثال، لنفترض أن جسمًا حرًا، لا تؤثر عليه أي قوة خارجية، يكون في حالة سكون في لحظة ما. وفي العديد من أنظمة الإحداثيات، يبدأ التحرك في اللحظة التالية، على الرغم من عدم وجود قوة تؤثر عليه. ومع ذلك، يمكن للمرء دائمًا اختيار إطار مرجعي يبقى فيه ثابتًا. وبالمثل، إذا لم يتم وصف المكان بشكل موحد أو الوقت بشكل مستقل، يمكن لنظام الإحداثيات وصف الرحلة البسيطة لجسم حر في الفضاء على أنها خط متعرج معقد في نظام الإحداثيات الخاص به. في الواقع، يمكن إعطاء ملخص مرئي لأطر القصور الذاتي: في الإطار المرجعي بالقصور الذاتي، تكون قوانين الميكانيكا في أبسط صورها.

وفقًا للمسلمة الأولى للنسبية الخاصة، فإن جميع القوانين الفيزيائية تأخذ أبسط أشكالها في إطار قصوري، وهناك إطارات قصورية متعددة ترتبط بترجمة موحدة:

مبدأ النسبية الخاصة: إذا تم اختيار نظام من الإحداثيات K بطريقة تجعل قوانين الفيزياء في أبسط صورها صالحة بالنسبة لأي نظام آخر من الإحداثيات K’ يتحرك نسبيًا مع ترجمة موحدة، فهي جيدة. ك.

– ألبرت أينشتاين: أسس النسبية العامة، الجزء أ، §1

تتجلى هذه البساطة في حقيقة أن إطارات القصور الذاتي لها فيزياء مستقلة دون الحاجة إلى أسباب خارجية، في حين أن فيزياء الإطارات غير القصورية لها أسباب خارجية. يمكن استخدام مبدأ البساطة في الفيزياء النيوتونية وكذلك في النسبية الخاصة. انظر ناجل [12] وكذلك بلاغوجيفيتش.

قوانين ميكانيكا نيوتن لا تبقى دائما في أبسط صورها… فلو، على سبيل المثال، تم وضع مراقب على قرص يدور بالنسبة للأرض، فإنه سيشعر بقوة تدفعه نحو الحافة. القرص، والذي لا ينتج عن أي تفاعل مع كائنات أخرى. هنا، التسارع ليس نتيجة القوة المعتادة، بل نتيجة ما يسمى بقوة القصور الذاتي. توجد قوانين نيوتن في أبسط صورها فقط في عائلة من الإطارات المرجعية تسمى إطارات القصور الذاتي. توضح هذه الحقيقة جوهر مبدأ النسبية لجاليليو:
قوانين الميكانيكا لها نفس الشكل في جميع إطارات القصور الذاتي.

– ميلوتين بلاغوجيفيتش: الجاذبية والتماثل، ص4

من الناحية العملية، يعني تكافؤ الإطارات المرجعية بالقصور الذاتي أن العلماء داخل صندوق متحرك بشكل منتظم لا يمكنهم تحديد سرعتهم المطلقة من خلال أي تجربة. وبخلاف ذلك، فإن الاختلافات تخلق إطارًا مرجعيًا قياسيًا مطلقًا. [14] [15] وفقًا لهذا التعريف، المكمل بثبات سرعة الضوء، فإن الإطارات المرجعية للقصور الذاتي تتغير فيما بينها وفقًا لتحولات تناظر بوانكاريه، والتي تعد تحويلات لورنتز مجموعة فرعية منها. [16] في الميكانيكا النيوتونية، والتي يمكن اعتبارها حالة محدودة من النسبية الخاصة حيث تكون سرعة الضوء لا نهائية، ترتبط الإطارات المرجعية بالقصور الذاتي بمجموعة التناظر الجاليلية.

الإطار المرجعي بالقصور الذاتي لنيوتن

الفضاء المطلق

اعتبر نيوتن الفضاء المطلق، والذي يتم تقريبه جيدًا من خلال إطار مرجعي ثابت بالنسبة للنجوم الثابتة. ثم كان الإطار بالقصور الذاتي فيما يتعلق بمساحة الترجمة المطلقة موحدًا. ومع ذلك، شعر بعض العلماء (الذي أطلق عليهم ماخ “النسبيون”)، حتى في زمن نيوتن، أن الفضاء المطلق كان عيبًا في الصياغة ويجب استبداله.

في الواقع، تمت صياغة مصطلح مرجع القصور الذاتي (بالألمانية: Inertialsystem) في عام 1885 من قبل لودفيج لانج ليحل محل تعريفات نيوتن “للمكان والزمان المطلقين” بتعريف أكثر عملية. [18] [19] كما ترجم إيرو، قدم لونغ التعريف التالي: [20]

الإطار المرجعي الذي يتم فيه رمي كتلة نقطية من نفس النقطة في ثلاثة اتجاهات مختلفة (غير متحدة المستوى) تتبع مسارات مستقيمة في كل مرة يتم رميها فيها يسمى الإطار بالقصور الذاتي.

يمكن العثور على مناقشة لاقتراح لانغ في ماخ.

وقد ذكر بلاغوجيفيتش عدم كفاية مفهوم “الفضاء المطلق” في الميكانيكا النيوتونية:

• إن وجود الفضاء المطلق يتناقض مع المنطق الداخلي للميكانيكا الكلاسيكية، لأنه وفقًا لمبدأ النسبية لجاليليو، لا يمكن فصل أي من إطارات القصور الذاتي.
• الفضاء المطلق لا يفسر قوى القصور الذاتي لأنها مرتبطة بالتسارع بالنسبة لأي إطار قصوري .
• يؤثر الفضاء المطلق على الأجسام المادية عن طريق تحفيز مقاومتها للتسارع، ولكن لا يمكن التأثير عليه.

– ميلوتين بلاغوجيفيتش: الجاذبية والتماثل، ص5

لقد تم استخدام التعريفات العملية في النظرية النسبية الخاصة بشكل أكبر بكثير. يتم توفير بعض الخلفية التاريخية، بما في ذلك تعريف لونج بواسطة Disall، والذي يلخص:

والسؤال الرئيسي هو: “ما هو الإطار المرجعي الذي توجد به قوانين الحركة؟” اتضح أن هذا خطأ. لأن قوانين الحركة تحدد بشكل أساسي فئة من الإطارات المرجعية و(من حيث المبدأ) طريقة لبنائها.

– المكان والزمان لروبرت د. سال: إطارات القصور الذاتي

الميكانيكا النيوتونية

النظريات الكلاسيكية التي تستخدم التحويل الجليلي تفترض تكافؤ جميع الأطر المرجعية بالقصور الذاتي. قد تفترض بعض النظريات وجود إطار مميز يوفر المكان المطلق والزمن المطلق. يحول التحويل الجليلي الإحداثيات من إطار مرجعي بالقصور الذاتي، s ، إلى إطار مرجعي قصوري آخر، s، عن طريق إضافة أو طرح الإحداثيات:

ص” = ص – ص 0 – الخامس ر

تي” = تي – تي 0

حيث تمثل r 0 وt 0 التغيرات في أصل المكان والزمان وv هي السرعة النسبية لإطارين مرجعيين بالقصور الذاتي. في ظل التحويلات الجليلية، الزمن t 2 − t 1 بين حدثين هو نفسه بالنسبة لجميع الإطارات المرجعية، والمسافة بين حدثين متزامنين (أو ما يعادلها، طول كل كائن، | r 2 − r 1 |) هي أيضًا نفس. نفس الشيء

الشكل 1: إطاران مرجعيان يتحركان بسرعة نسبية v → . يحتوي الإطار S على دوران تعسفي ولكن ثابت مقارنة بالإطار S. كلاهما إطاران بالقصور الذاتي بشرط أن يتحرك الجسم الذي لا يتأثر بالقوة في خط مستقيم. إذا شوهدت تلك الحركة في إطار واحد، فسوف تظهر بنفس الطريقة في إطار آخر.

في عالم الميكانيكا النيوتونية، الإطار المرجعي بالقصور الذاتي أو الإطار المرجعي بالقصور الذاتي هو الإطار الذي يكون فيه قانون نيوتن الأول للحركة صالحًا. [24] ومع ذلك، فإن مبدأ النسبية الخاصة يوسع مفهوم إطار القصور الذاتي ليشمل جميع القوانين الفيزيائية، وليس فقط قانون نيوتن الأول.

واعتبر نيوتن أن القانون الأول صالح في أي إطار مرجعي يتحرك بشكل منتظم بالنسبة للنجوم الثابتة. [25] أي لا يدور ولا يتسارع بالنسبة إلى النجوم. [26] واليوم تم التخلي عن مفهوم “الفضاء المطلق” وتم تعريف إطار القصور الذاتي في مجال الميكانيكا الكلاسيكية على النحو التالي: [27] [28]

الإطار المرجعي بالقصور الذاتي هو الإطار الذي تكون فيه حركة الجسيم الذي لا يتأثر بالقوى في خط مستقيم وبسرعة ثابتة.

وهكذا، وفقًا لإطار القصور الذاتي، فإن الجسم أو الأجسام تتسارع فقط عند تطبيق قوة فيزيائية، و(وفقًا لقانون نيوتن الأول للحركة)، في حالة عدم وجود قوة محصلة، يظل الجسم الساكن ساكنًا. سيستمر الجسم في الحركة بشكل منتظم، أي في خط مستقيم وبسرعة ثابتة. تتحول إطارات القصور الذاتي النيوتونية فيما بينها وفقًا لمجموعة التناظر الجليلية.

إذا تم تفسير هذا القانون على أنه يعني أن الحركة في خط مستقيم تمثل قوة صافية صفر، فإن القانون لا يتعرف على الإطارات المرجعية بالقصور الذاتي لأنه يمكن ملاحظة حركة الخط المستقيم في مجموعة متنوعة من الإطارات. إذا تم تفسير القانون على أنه يحدد إطارًا بالقصور الذاتي، فيجب أن نكون قادرين على تحديد متى يتم تطبيق قوة صافية صفرية. وقد لخص أينشتاين هذه المشكلة في: [29]

تكمن نقطة الضعف في مبدأ القصور الذاتي في أنه ينطوي على التفكير في دائرة: يتحرك الجسم دون تسارع إذا كان بعيدًا بدرجة كافية عن الأجسام الأخرى. نحن نعلم أنه بعيد بما فيه الكفاية عن الأجسام الأخرى فقط لأنه يتحرك دون تسارع.

— ألبرت أينشتاين: معنى النسبية، ص. 58

هناك عدة طرق لهذا. أحد الأساليب هو القول بأن جميع القوى الحقيقية تتناقص مع المسافة من مصادرها بطريقة معروفة، لذلك نحتاج فقط إلى التأكد من أن الجسم بعيد بما يكفي عن جميع المصادر للتأكد من عدم وجود قوى. [30] إحدى المشاكل المحتملة في هذا النهج هي النظرة التاريخية القديمة القائلة بأن العالم البعيد قد يؤثر على الأشياء (مبدأ ماخ). هناك طريقة أخرى تتمثل في تحديد جميع المصادر الحقيقية للقوى الحقيقية وحسابها. المشكلة المحتملة في هذا النهج هي أننا قد نفتقد شيئًا ما، أو ربما، مرة أخرى، بسبب مبدأ ماخ وفهمنا غير الكامل للكون، نعتبر تأثيرها بشكل غير مناسب. النهج الثالث هو النظر في كيفية تغير القوى عندما تتغير الأطر المرجعية. القوى الوهمية، تلك الناجمة عن تسارع الإطار، تختفي في الإطارات القصورية، وبشكل عام لها قوانين تحويل معقدة. واستنادا إلى عالمية القانون الفيزيائي والطلب على الأطر التي يتم فيها ذكر القوانين ببساطة، تتميز الأطر بالقصور الذاتي بغياب مثل هذه القوى الاصطناعية.

وقد عبّر نيوتن نفسه عن مبدأ النسبية في إحدى نتائجه المتعلقة بقوانين الحركة: [31] [32]

إن حركات الأجسام في فضاء معين هي نفسها فيما بينها، سواء كان ذلك الفضاء ساكنًا أو يتحرك بشكل منتظم للأمام في خط مستقيم.

– إسحاق نيوتن: المبادئ، الخاتمة الخامسة، ص١٤٤. 88 في ترجمة أندرو موت

ويختلف هذا المبدأ عن المبدأ الخاص من ناحيتين: أولاً، أنه خاص بالميكانيكا، وثانياً، أنه لا يشير إلى البساطة. يُترجم هذا المبدأ الخاص إلى ثبات شكل الوصف بين أطر الإسناد الترافقي. [33] يتم متابعة دور القوى الوهمية في تصنيف الأطر المرجعية.

صياغات

ومن المهم أن نلاحظ بعض الافتراضات المذكورة أعلاه حول مختلف الأطر المرجعية بالقصور الذاتي. على سبيل المثال، استخدم نيوتن التوقيت العالمي، كما هو موضح في المثال أدناه. لنفترض أنك تمتلك ساعتين تدق كل منهما بنفس المعدل تمامًا. يمكنك مزامنتهما بحيث يتم عرضهما في نفس الوقت تمامًا. الآن تم فصل الساعتين وإحدى الساعتين في قطار متحرك يتحرك بسرعة ثابتة تجاه الأخرى. وفقًا لنيوتن، ستظل الساعتان تدقان بنفس المعدل وستعرضان نفس الوقت. يقول نيوتن (ما هو قانون القصور الذاتي) أن معدل الزمن المقاس في إطار مرجعي واحد يجب أن يكون هو نفس معدل الزمن في إطار مرجعي آخر. أي أن هناك وقتًا “عالميًا”، وجميع الأوقات الأخرى في جميع الإطارات المرجعية الأخرى تعمل بنفس سرعة الوقت العالمي، بغض النظر عن موقعها وسرعتها. تم توسيع مفهوم الوقت والتزامن لاحقًا بواسطة أينشتاين في نظريته النسبية الخاصة (1905) حيث أجرى تحويلات بين الأطر المرجعية بالقصور الذاتي بناءً على الطبيعة العالمية للقوانين الفيزيائية والاقتصاد في التعبير عنها. تحويلات لورنتز).

تعتبر الإطارات المرجعية مهمة بشكل خاص في النسبية الخاصة، لأنه عندما يتحرك إطار مرجعي بجزء كبير من سرعة الضوء، فإن تدفق الوقت في هذا الإطار لا ينطبق بالضرورة على إطار آخر. تعتبر سرعة الضوء هي الثابت الحقيقي الوحيد بين الإطارات المرجعية المتحركة.

يمكن توسيع تعريف الإطار المرجعي بالقصور الذاتي إلى ما هو أبعد من الفضاء الإقليدي ثلاثي الأبعاد. افترض نيوتن الفضاء الإقليدي، لكن النسبية العامة تستخدم هندسة أكثر عمومية. وكمثال على أهمية ذلك، فكر في هندسة القطع الناقص. في هذه الهندسة، يتم تعريف الجسيم “الحر” على أنه جسيم ساكن أو يتحرك بسرعة ثابتة على طول المسار الجيوديسي. قد يبدأ جسيمان حران من نفس النقطة على السطح ويتحركان في اتجاهات مختلفة بنفس السرعة الثابتة. وبعد مرور بعض الوقت، يصطدم هذان الجسيمان على جانبين متقابلين من القطع الناقص. كان كلا الجسيمين “الحرة” يتحركان بسرعة ثابتة، مما يتوافق مع تعريف عدم وجود قوى تؤثر عليهما. ولم يحدث أي تسارع، وبالتالي كان قانون نيوتن الأول صحيحًا. وهذا يعني أن الجسيمات كانت في إطار مرجعي بالقصور الذاتي. وبما أنه لا توجد قوى مؤثرة، فإن هندسة الموقع هي التي تسببت في التقاء الجسيمين مرة أخرى. وبطريقة مماثلة، أصبح من الشائع الآن وصف [34] أننا موجودون في هندسة رباعية الأبعاد تسمى الزمكان. في هذه الصورة، انحناء هذا الفضاء رباعي الأبعاد هو المسؤول عن الطريقة التي يقترب بها جسمان لهما كتلة من بعضهما البعض، على الرغم من عدم وجود قوة تؤثر عليهما. يحل هذا الانحناء في الزمكان محل القوة المعروفة بالجاذبية في ميكانيكا نيوتن والنسبية الخاصة.

النسبية الخاصة (ما هو قانون القصور الذاتي) 

نظرية النسبية الخاصة لأينشتاين، مثل ميكانيكا نيوتن، تفترض تكافؤ جميع الأطر المرجعية بالقصور الذاتي. ومع ذلك، بما أن النسبية الخاصة تفترض أن سرعة الضوء في الفضاء الحر ثابتة، فإن التحول بين إطارات القصور الذاتي هو تحويل لورنتز، وليس التحويل الجليلي المستخدم في الميكانيكا النيوتونية. يؤدي ثبات سرعة الضوء إلى ظواهر غير بديهية مثل تمدد الزمن وتقلص الطول ونسبية التزامن، والتي تم التحقق منها على نطاق واسع تجريبيًا. [35] عندما تقترب سرعة الضوء من اللانهاية أو عندما تقترب السرعة النسبية بين الإطارات من الصفر، فإن تحويل لورنتز يختزل إلى التحويل الجليلي. [36]

إطارات غير بالقصور الذاتي

هنا يتم النظر في العلاقة بين الأطر المرجعية للرصد بالقصور الذاتي وغير بالقصور الذاتي. والفرق الرئيسي بين هذه الإطارات هو الحاجة إلى إطارات غير قصورية لقوى وهمية، وهو ما سيتم شرحه أدناه.

النسبية العامة

تعتمد النسبية العامة على مبدأ التكافؤ:

لا يوجد اختبار يستطيع المراقبون من خلاله معرفة ما إذا كان التسارع ناتجًا عن الجاذبية أم أن إطارهم المرجعي يتسارع.

— دوغلاس سي. جيانكولي، الفيزياء للعلماء والمهندسين مع الفيزياء الحديثة، ص. 155.

تم تقديم هذه الفكرة في ورقة أينشتاين عام 1907 بعنوان “مبدأ النسبية والجاذبية” وتم تطويرها لاحقًا في عام 1911. تم العثور على دعم لهذا المبدأ في تجربة إيوتفوس، التي تحدد ما إذا كانت نسبة كتلة القصور الذاتي إلى كتلة الجاذبية هي نفسها بالنسبة للجميع. الجسم بغض النظر عن حجمه أو تكوينه. حتى الآن، لم يتم العثور على اختلافات في حلقات متعددة في 10 11 . للاطلاع على بعض المناقشات حول التفاصيل الدقيقة لتجربة إيوتفوس، مثل توزيع الكتلة المحلية حول موقع التجربة (بما في ذلك الإشارة إلى كتلة إيوتفوس نفسها)، انظر فرانكلين.

تعدل نظرية أينشتاين العامة التمييز بين التأثيرات “القصورية” و”غير القصورية” الاسمية عن طريق استبدال فضاء مينكوفسكي “المسطح” للنسبية الخاصة بمقياس ينتج انحناء غير صفري. في النسبية العامة، يتم استبدال مبدأ القصور الذاتي بمبدأ الحركة الجيوديسية، حيث تتحرك الأجسام بطريقة يمليها انحناء الزمكان. ونتيجة لهذا الانحناء، ليس من الواضح في النسبية العامة أن الأجسام بالقصور الذاتي التي تتحرك بسرعة معينة بالنسبة لبعضها البعض سوف تستمر في الحركة. تعني ظاهرة الانحراف الجيوديسي أن الأطر المرجعية بالقصور الذاتي مثل ميكانيكا نيوتن والنسبية الخاصة غير موجودة.

ومع ذلك، فإن النظرية العامة تختزل إلى نظرية محددة في مناطق صغيرة بما فيه الكفاية من الزمكان، حيث تصبح تأثيرات الانحناء أقل أهمية ويمكن أن تلعب حجج إطار القصور الذاتي البدائي دورًا مرة أخرى. ونتيجة لذلك، توصف النسبية الخاصة الحديثة الآن بأنها “نظرية محلية” فقط. “محلي” يمكن أن يشمل، على سبيل المثال، مجرة ​​درب التبانة بأكملها: لاحظ عالم الفلك كارل شوارزشيلد حركة أزواج من النجوم تدور حول بعضها البعض. ووجد أن مداري النجمين في مثل هذا النظام يقعان في نفس المستوى وأن الحضيض لمدارات النجمين في نفس الاتجاه بالنسبة للنظام الشمسي. وأشار شوارزشيلد إلى أن هذا هو الحال دائمًا: يظل اتجاه الحركة الزاوية لجميع أنظمة النجوم الثنائية المرصودة ثابتًا بالنسبة لاتجاه الحركة الزاوية للنظام الشمسي.

إطارات القصور الذاتي والدوران (ما هو قانون القصور الذاتي) 

في إطار القصور الذاتي، يتم استيفاء قانون نيوتن الأول، قانون القصور الذاتي: كل حركة حرة لها مقدار واتجاه ثابتان. قانون نيوتن الثاني للجسيم هو كما يلي:

F = متر أ،

مع F القوة الصافية (المتجه)، الجسيم (أيضًا m هي كتلة الجسيم و a هو ناقل التسارع) يتم قياسه بواسطة مراقب في حالة سكون في الإطار. القوة F هي المجموع المتجه لجميع القوى “الحقيقية” المؤثرة على الجسيم، مثل قوى التلامس والكهرومغناطيسية والجاذبية والقوى النووية.

في المقابل، قانون نيوتن الثاني في الإطار المرجعي الدوار (إطار مرجعي غير قصوري)، الذي يدور حول محور بسرعة زاوية Ω، هو كما يلي:

F = متر أ،

والذي يبدو كإطار قصوري، لكن القوة F’ هي حاصل ضرب ليس فقط F ولكن مصطلحات إضافية (الفقرة التالية من هذه المعادلة تعطي الجوهر بدون الرياضيات الدقيقة):

F ” = F – 2 م OH × v B – م OH × (OH × X B) – م د OH D T × X B،

حيث يُشار إلى الدوران الزاوي للمربع بواسطة المتجه Ω، الذي يكون في اتجاه محور الدوران، وله حجم يساوي معدل الدوران الزاوي Ω، ويشير الرمز x إلى منتج المتجه، المتجه x B يمثل الجسم، والمتجه v B هو سرعة الجسم بالنسبة إلى مراقب دوار (يختلف عن السرعة التي يلاحظها مراقب قصوري).

المصطلحات الإضافية في القوة F هي قوى “زائفة” لهذا الإطار والتي تكون أسبابها خارجية بالنسبة للنظام الموجود في الإطار. الحد الإضافي الأول هو قوة كوريوليس، والثاني هو قوة الطرد المركزي، والثالث هو قوة أويلر. جميع هذه التعبيرات لها الخصائص التالية: تختفي عندما تكون Ω = 0. أي أنها صفر بالنسبة لإطار بالقصور الذاتي (والذي، بالطبع، لا يدور). إنها تفترض قيمة واتجاهًا مختلفين اعتمادًا على القيمة المحددة لـ Ω في كل إطار دوار. فهي منتشرة في كل مكان في الإطار الدوار (تؤثر على كل جسيم، بغض النظر عن حالته). ليس لديهم أي مصدر واضح في المصادر المادية التي يمكن تحديدها، وخاصة المادة. كما أن القوى الوهمية لا تختفي مع المسافة (على عكس القوى النووية أو القوى الكهربائية على سبيل المثال). على سبيل المثال، قوة الطرد المركزي التي يبدو أنها تنبعث من محور الدوران في إطار دوار، تزداد مع المسافة من المحور.

يتفق جميع المراقبين على القوى الحقيقية F.، فقط المراقبون غير القصوريين هم الذين يحتاجون إلى قوى وهمية. تكون قوانين الفيزياء أبسط في إطار القصور الذاتي لأنه لا توجد قوى غير ضرورية.

في زمن نيوتن، تم استخدام النجوم الثابتة كإطار مرجعي، ويبدو أنها في حالة سكون بالنسبة إلى الفضاء المطلق. في الأطر المرجعية التي كانت إما في حالة سكون بالنسبة إلى النجوم الثابتة أو في ترجمة موحدة بالنسبة لهذه النجوم، كانت قوانين نيوتن للحركة موجودة. في المقابل، في الإطارات المتسارعة بالنسبة إلى النجوم الثابتة، وهي حالة مهمة من الإطارات التي تدور بالنسبة إلى النجوم الثابتة، لم تظل قوانين الحركة في أبسط أشكالها، ولكن كان لا بد من استكمالها بإضافة قوى وهمية. على سبيل المثال، قوة كوريوليس وقوة الطرد المركزي. ابتكر نيوتن تجربتين ليبين كيف يمكن اكتشاف هذه القوى، وبذلك يظهر للراصد أنها لم تكن في إطار قصوري: مثال التوتر في الحبل السري الذي يسحب كرتين تدوران حول مركز ثقلهما؛ ومثال انحناء سطح الماء في دلو دوار.

وكما نعلم الآن، فإن النجوم الثابتة ليست ثابتة. أولئك الذين يعيشون في درب التبانة يدورون مع المجرة ويظهرون الحركات المناسبة. تلك الموجودة خارج مجرتنا (مثل السدم التي كان يُعتقد خطأً أنها نجوم) تشارك أيضًا في حركتها، ويرجع ذلك جزئيًا إلى توسع الكون، وجزئيًا بسبب السرعات الغريبة. [46] على سبيل المثال، مجرة ​​المرأة المسلسلة في مسار تصادمي مع مجرة ​​درب التبانة بسرعة 117 كم/ثانية. لم يعد مفهوم الإطارات المرجعية بالقصور الذاتي مرتبطًا بالنجوم الثابتة أو الفضاء المطلق. بل إن تحديد إطار القصور الذاتي يعتمد على بساطة قوانين الفيزياء الموجودة في الإطار. كتب جون ستاتشيل: بمجرد أن تخلى عن وجود إطار مرجعي متميز (إطار الأثير)، لم يكن هناك سبب للتوقف عند نسبية الإطارات القصورية.

من الناحية العملية، على الرغم من أن ذلك ليس مطلوبًا، إلا أن استخدام إطار مرجعي ثابت قائم على النجوم كما لو كان إطارًا مرجعيًا بالقصور الذاتي لا يحدث فرقًا كبيرًا. على سبيل المثال، فإن التسارع الطارد المركزي للأرض بسبب دورانها حول الشمس أكبر بنحو 30 مليون مرة من تسارع الشمس في مركز المجرة.

لمزيد من التوضيح، فكر في السؤال: “هل يدور عالمنا؟” للحصول على إجابة، قد نحاول تفسير شكل مجرة ​​درب التبانة باستخدام قوانين الفيزياء، [50] على الرغم من أن الملاحظات الأخرى قد تكون أكثر حسمًا. وهذا يعني وجود تناقضات أكبر أو عدم يقين أقل في القياس، مثل تباين إشعاع الخلفية الميكروي أو الاندماج النووي للانفجار الكبير. يعتمد استواء مجرة ​​درب التبانة على سرعة دورانها في إطار مرجعي بالقصور الذاتي. إذا نسبنا معدل دورانه الظاهري بالكامل إلى الدوران في إطار قصوري، فمن المتوقع حدوث “سلاسة” مختلفة عما لو افترضنا أن جزءًا من هذا الدوران يرجع في الواقع إلى دوران الكون ولا ينبغي تضمينه في دوران الكون. المجرة. بناءً على قوانين الفيزياء، تم وضع نموذج تكون فيه إحدى المعلمات هي سرعة دوران الكون. إذا كانت قوانين الفيزياء تتفق بشكل أفضل مع الملاحظات في نموذج ذو دوران أكثر من عدمه، فإننا نميل إلى اختيار أفضل قيمة للدوران، مع مراعاة الملاحظات التجريبية الأخرى ذات الصلة. إذا لم تكن أي قيمة لمعلمة الدوران ناجحة ولم تكن النظرية ضمن خطأ المراقبة، فسيتم النظر في تعديل القانون الفيزيائي، على سبيل المثال، يتم استدعاء المادة المظلمة لشرح منحنى دوران المجرة. حتى الآن، تشير الملاحظات إلى أن أي دوران في الكون يكون بطيئًا جدًا، ولا يزيد سرعته عن مرة واحدة كل 6 × 10 13 سنة (10-13 راد في السنة)، ويوجد جدل حول ما إذا كان الدوران مستمرًا. ومع ذلك، إذا تم العثور على الدوران، فإن تفسير الملاحظات في إطار محدد كونيًا يجب تصحيحه للقوى الزائفة الموجودة في مثل هذا الدوران في الفيزياء الكلاسيكية والنسبية الخاصة، أو تفسيره على أنه انحناء الزمكان وحركة المادة على طول هو – هي. الجيوديسيا في النسبية العامة حتى الآن، تشير الملاحظات إلى أن أي دوران في الكون يكون بطيئًا جدًا، ولا يزيد سرعته عن مرة واحدة كل 6 × 10 13 سنة (10-13 راد في السنة)، ويوجد جدل حول ما إذا كان الدوران مستمرًا. ومع ذلك، إذا تم العثور على الدوران، فإن تفسير الملاحظات في إطار محدد كونيًا يجب تصحيحه للقوى الزائفة الموجودة في مثل هذا الدوران في الفيزياء الكلاسيكية والنسبية الخاصة، أو تفسيره على أنه انحناء الزمكان وحركة المادة على طول هو – هي. الجيوديسيا في النسبية العامة حتى الآن، تشير الملاحظات إلى أن أي دوران في الكون يكون بطيئًا جدًا، ولا يزيد سرعته عن مرة واحدة كل 6 × 10 13 سنة (10-13 راد في السنة)، ويوجد جدل حول ما إذا كان الدوران مستمرًا. ومع ذلك، إذا تم العثور على الدوران، فإن تفسير الملاحظات في إطار محدد كونيًا يجب تصحيحه للقوى الزائفة الموجودة في مثل هذا الدوران في الفيزياء الكلاسيكية والنسبية الخاصة، أو تفسيره على أنه انحناء الزمكان وحركة المادة على طول هو – هي. الجيوديسيا في النسبية العامة

عندما تكون التأثيرات الكمومية مهمة، تنشأ تعقيدات مفاهيمية أخرى في الأطر المرجعية الكمومية.

الإطارات الأولية (ما هو قانون القصور الذاتي) 

غالبًا ما يتم تحديد الإطار المرجعي المتسارع باعتباره الإطار “الستاري”، ويتم الإشارة إلى جميع المتغيرات المعتمدة على هذا الإطار بواسطة أرقام أولية، على سبيل المثال x’ , y’ , a’ .

يُشار عادةً إلى المتجه من أصل الإطار المرجعي بالقصور الذاتي إلى أصل الإطار المرجعي المتسارع بالرمز R. وفقا لنقطة الاهتمام في كلا الإطارين، يسمى المتجه من أصل القصور الذاتي إلى النقطة r ويسمى المتجه من أصل التسارع إلى النقطة r’. نحصل على الموقف من الهندسة

ص = ص + ص “.

وبأخذ المشتقتين الأولى والثانية من هذا بالنسبة للزمن، نحصل على ذلك

الخامس = الخامس + الخامس “،

أ = أ + أ.

حيث V و A هما سرعة وتسارع نظام التسارع بالنسبة إلى إطار القصور الذاتي و v و a هما سرعة وتسارع النقطة المطلوبة بالنسبة إلى إطار القصور الذاتي.

تسمح هذه المعادلات بالتحويل بين نظامين إحداثيين. على سبيل المثال، يمكننا الآن كتابة قانون نيوتن الثاني

F = متر أ = متر أ + متر أ.

عندما يتم تسريع الحركة بسبب القوة المطبقة، فهذا مظهر من مظاهر القصور الذاتي. إذا كانت السيارة الكهربائية، المصممة لإعادة شحن نظام بطاريتها عند التباطؤ، تستخدم المكابح، فسيتم إعادة شحن البطاريات، مما يدل على القوة الجسدية لإظهار القصور الذاتي. ومع ذلك، فإن مظاهر القصور الذاتي لا تمنع التسارع (أو التباطؤ)، لأن مظاهر القصور الذاتي تحدث استجابة لتغير السرعة بسبب القوة. من منظور الإطار المرجعي الدوار، يبدو مظهر القصور الذاتي وكأنه يمارس قوة (إما في اتجاه الطرد المركزي، أو في الاتجاه العمودي على حركة الجسم، وهو تأثير كوريوليس).

النوع الشائع من الإطار المرجعي المتسارع هو الإطار الذي يدور ويترجم في نفس الوقت (على سبيل المثال، إطار مرجعي متصل بقرص مضغوط يتم تشغيله أثناء حمل المشغل). يؤدي هذا الترتيب إلى المعادلة (انظر القوة الوهمية للمشتقة):

А = А” + ОИ ˙ × r” + 2 ОО × v” + Ох × (О× × r”) + А 0،

أو، لحل مشكلة التسارع في إطار التسارع،

أ” = أ – أوه˙ × ص” – 2 أوه × v” – أوه × (أوه × ص”) – أ 0.

يتم الحصول على الضرب بالكتلة m

“F” = FP Hour y S M J A L + F E إلى l h r ” + FC أو M o l M s ” + FJ n T r Mn p t ial ” – متر A 0،

أين

F E إلى l h r” = – متر˙ x r” (قوة أويلر)

FC أو I O L I S” = – 2 m OH × v” (قوة كوريوليس)،

fj n ti r i f to g al l” = – m o × (oh × r”) = m (oh 2 r” – (oh ⋅ r”) oh) (قوة الطرد المركزي) .

فصل الأطر المرجعية غير بالقصور الذاتي عن الأطر المرجعية بالقصور الذاتي

نظرية

يمكن تمييز الأطر المرجعية بالقصور الذاتي وغير بالقصور الذاتي بغياب أو وجود قوى وهمية كما هو موضح بإيجاز. [9] [10]

وتأثير هذا الوجود في الإطار غير القصوري هو أنه يتطلب من الراصد إدخال قوة وهمية في حساباته.

– سيدني بورويتز ولورانس بورنشتاين في رؤية معاصرة للفيزياء الابتدائية، ص. 138

يوضح وجود القوى الوهمية أن القوانين الفيزيائية ليست أبسط القوانين المتاحة، وبالتالي، وفقًا لمبدأ النسبية الخاصة، فإن الإطار الذي توجد فيه القوى الوهمية ليس إطارًا بالقصور الذاتي:

تختلف معادلات الحركة في نظام غير بالقصور الذاتي عن معادلات نظام القصور الذاتي بمصطلحات إضافية تسمى قوى القصور الذاتي. وهذا يسمح لنا بالتعرف تجريبيًا على الطبيعة غير القصورية للنظام.

— VI أرنولد: الطرق الرياضية للميكانيكا الكلاسيكية الطبعة الثانية، ص. 129

تخضع الأجسام الموجودة في الأطر المرجعية غير القصورية لما يسمى بالقوى الوهمية (القوى الزائفة). أي أن القوى الناتجة عن تسارع الإطار المرجعي وليس عن القوة الفيزيائية المؤثرة على الجسم. ومن أمثلة القوى الوهمية قوة الطرد المركزي وقوة كوريوليس في الإطارات المرجعية الدوارة.

فكيف نفصل القوى “الزائفة” عن القوى “الحقيقية”؟ ومن الصعب تطبيق التعريف النيوتوني للإطار بالقصور الذاتي دون هذا الفصل. على سبيل المثال، فكر في جسم ثابت في إطار بالقصور الذاتي. في حالة الراحة، لا يتم تطبيق أي قوة صافية. لكن في الإطار الذي يدور حول محور ثابت، يبدو الجسم وكأنه يتحرك في دائرة ويخضع لقوة الجذب المركزي (التي تتكون من قوة كوريوليس وقوة الطرد المركزي). كيف يمكننا أن نقرر أن الإطار الدوار هو إطار غير قصوري؟ هناك طريقتان لهذا الحل: أحدهما هو البحث عن أصل القوى الوهمية (قوة كوريوليس والقوة الطاردة المركزية). وسنجد أنه لا يوجد مصدر لهذه القوى، ولا حامل قوة مرتبط بها، ولا جهة مصدرها. [56] النهج الثاني هو النظر إلى مجموعة متنوعة من الأطر المرجعية. بالنسبة لأي إطار قصوري، تختفي قوة كوريوليس وقوة الطرد المركزي، وبالتالي فإن تطبيق مبدأ النسبية الخاصة يحدد هذه الإطارات التي تختفي فيها القوى باعتبارها قوانين فيزيائية شائعة، ومن ثم يفرض أن الإطار الدوار هو إطار. انها ليست الدورية. إطار القصور الذاتي

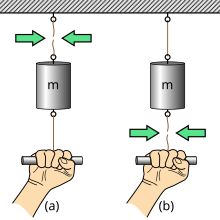
وقد بحث نيوتن بنفسه في هذه المشكلة باستخدام الكرات الدوارة، كما هو موضح في الشكل 2 والشكل 3. وأشار إلى أنه إذا لم تكن الكرات تدور، فإن التوتر في سلسلة الوصلة سيكون قياسه صفرًا في أي إطار مرجعي. [57] إذا بدت الكرات وكأنها تدور فقط (أي نلاحظ الكرات الثابتة من إطار دوار)، فإن التوتر في الخيط يكون صفرًا، مع ملاحظة أن قوة الطرد المركزي يتم توفيرها من خلال قوى الطرد المركزي وقوات كوريوليس مجتمعة. كن محل ثقة. ، فلا داعي للتوتر. إذا كانت الكرات تدور بالفعل، فإن السحب المرصود هو بالضبط قوة الجذب المركزي المطلوبة للحركة الدائرية. وبالتالي، فإن قياس التوتر في الوتر يحدد إطار القصور الذاتي: أي الإطار الذي يوفر فيه التوتر في الوتر بالضبط قوة الجذب المركزي المطلوبة للحركة كما هو موضح في ذلك الإطار، وليس بعض القيمة المختلفة. أي أن إطار القصور الذاتي هو الإطار الذي تختفي فيه القوى الوهمية.

الكثير بالنسبة للقوى الوهمية بسبب الدوران. ومع ذلك، بالنسبة للتسارع الخطي، عبر نيوتن عن فكرة مراوغة حول التسارعات المستقيمة الشائعة:[32]

إذا تحركت الأجسام، مهما كانت متحركة فيما بينها، في خطوط متوازية بواسطة قوى تسارع متساوية، فإنها تستمر في الحركة فيما بينها، بنفس الطريقة كما لو لم تؤثر عليها أي قوة.

– إسحاق نيوتن: خاتمة المبدأ السادس، ص٢٤. 89، ترجمة أندرو موت

هذا المبدأ يعمم مفهوم الإطار بالقصور الذاتي. على سبيل المثال، يدعي مراقب محاصر في مصعد سقوط حر أنه في حد ذاته إطار قصوري صحيح، على الرغم من أنه يتسارع تحت قوة الجاذبية، حتى لا يكون لديه أي معلومات عن أي شيء خارج المصعد. لذلك، بالمعنى الدقيق للكلمة، فإن إطار القصور الذاتي هو مفهوم نسبي. مع أخذ ذلك في الاعتبار، يمكن تعريف إطارات القصور الذاتي على أنها مجموعة من الإطارات الثابتة بالنسبة لبعضها البعض أو تتحرك بسرعة ثابتة، بحيث يتم تعريف إطار القصور الذاتي كعنصر من عناصر هذه المجموعة.

لتطبيق هذه الأفكار، يجب أن يخضع كل شيء يتم عرضه في الإطار لخط أساس مشترك وتسارع مشترك بين الإطار نفسه. هذا هو الحال، على سبيل المثال، مع مثال المصعد، حيث تخضع جميع الأجسام لنفس تسارع الجاذبية، والمصعد نفسه يتسارع بنفس المعدل.

تطبيقات (ما هو قانون القصور الذاتي) 

تستخدم أنظمة الملاحة بالقصور الذاتي مجموعة من الجيروسكوبات ومقاييس التسارع لتحديد التسارع بالنسبة إلى الفضاء بالقصور الذاتي. بعد أن يتم تدوير الجيروسكوب في اتجاه معين في الفضاء بالقصور الذاتي، يتطلب قانون الحفاظ على الزخم الزاوي أن يحافظ على هذا الاتجاه طالما لا تؤثر عليه أي قوة خارجية. [58] : 59 تقوم ثلاثة جيروسكوبات متعامدة بإنشاء إطار مرجعي بالقصور الذاتي وتقوم مقاييس التسارع بقياس التسارع بالنسبة لهذا الإطار. ومن ثم يمكن استخدام التسارع مع الساعة لحساب تغير الموضع. ولذلك، فإن الملاحة بالقصور الذاتي هي شكل من أشكال الحساب الميت الذي لا يتطلب أي مدخلات خارجية وبالتالي لا يمكن حظره بواسطة أي مصدر إشارة خارجي أو داخلي. [59]

البوصلة الجيروسكوبية، المستخدمة في ملاحة السفن في البحر، تحدد موقع الشمال هندسيًا. وهو لا يفعل ذلك عن طريق قياس المجال المغناطيسي للأرض، ولكن باستخدام الفضاء بالقصور الذاتي كمرجع له. يتم تثبيت الغلاف الخارجي للجيروسكوب بطريقة تظل متماشية مع الخط الراسيا المحلي. عندما تدور عجلة الجيروسكوب داخل الجيروسكوب للأعلى، فإن الطريقة التي يتم بها تعليق عجلة الجيروسكوب تجعل عجلة الجيروسكوب تحاذي محور دورانها تدريجيًا مع محور الأرض. إن المحاذاة مع محور الأرض هي الاتجاه الوحيد الذي يمكن من خلاله تثبيت محور دوران الجيروسكوب بالنسبة للأرض ولا داعي لتغيير الاتجاه بالنسبة للفضاء القصوري. وبعد الدوران يستطيع الجيروسكوب أن يحاذي محور الأرض خلال ربع ساعة. [60]

أمثلة (ما هو قانون القصور الذاتي) 

ولم يذكر أي مصدر في هذا القسم. الرجاء المساعدة في تحسين هذا القسم عن طريق إضافة الاستشهادات إلى المصادر الموثوقة. قد يتم تحدي المحتوى غير المصدر وإزالته. (يوليو 2013) ( تعرف على كيفية ووقت حذف رسالة القالب هذه )

مثال بسيط

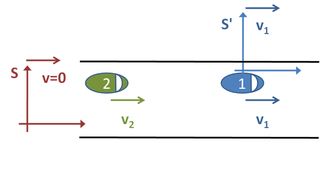
النظر في الوضع المشترك في الحياة اليومية. تسير سيارتان على نفس الطريق، وتتحرك كلتاهما بسرعة ثابتة. انظر الشكل 1. في لحظة معينة، يتم فصلهم بمقدار 200 متر. تتحرك السيارة الأمامية بسرعة ٢٢ م/ث، والسيارة الخلفية تتحرك بسرعة ٣٠ م/ث. إذا أردنا معرفة المدة التي ستستغرقها السيارة الثانية للوصول إلى السيارة الأولى، فهناك ثلاثة “أطر مرجعية” واضحة يمكننا الاختيار من بينها. [61]

أولاً، تمكنا من رؤية سيارتين من جانب الطريق. نحدد “الإطار المرجعي” الخاص بنا S على النحو التالي. نتوقف على جانب الطريق ونشغل ساعة الإيقاف في نفس اللحظة التي تمر فيها السيارة الثانية بنا، وذلك عندما تكون المسافة بينهما d = 200 متر. نظرًا لعدم تسارع أي سيارة، يمكننا تحديد موضعها باستخدام الصيغ التالية: x1 (t) هو موضع السيارة بالأمتار واحدة بعد الزمن t بالثواني وx2 (t) هو موضع السيارة اثنين بعد الزمن t هو

X 1 (t) = d + v 1 t = 200 + 22 t، x 2 (t) = v 2 t = 30 t.

لاحظ أن هذه الصيغ تتوقع أنه عند t = 0، تكون السيارة الأولى على مسافة 200 متر على الطريق والسيارة الثانية بجوارنا مباشرةً، كما هو متوقع. نريد إيجاد الوقت الذي يكون فيه x1 = x2 . لذلك، قمنا بتعيين x1 = x2 وحل من أجل t ، مما يعني أن:

200 + 22 طن = 30 طن،

8 طن = 200،

ر = 25 ث ح ج على د ث .

وبدلاً من ذلك، يمكننا اختيار الإطار المرجعي S’ الموجود في السيارة الأولى. في هذه الحالة، تكون السيارة الأولى ثابتة والسيارة الثانية تقترب من الخلف بسرعة v 2 − v 1 = 8 m/s. للوصول إلى السيارة الأولى يستغرق الزمن d/v2 – v1 = 8.200 ثانية. قبل، على سبيل المثال، 25 ثانية، لاحظ مدى سهولة المشكلة عن طريق اختيار إطار مرجعي مناسب. يتم إرفاق الإطار المرجعي الثالث المحتمل بالجهاز الثاني. هذا المثال مشابه للمثال الذي تمت مناقشته سابقًا، فيما عدا أن السيارة الثانية ثابتة والسيارة الأولى تتحرك للخلف بسرعة 8 م/ث.

كان من الممكن اختيار إطار مرجعي دوار ومتسارع يتحرك بطريقة معقدة، لكن هذا كان سيؤدي إلى تعقيد المشكلة دون داع. وتجدر الإشارة أيضًا إلى أنه يمكن تحويل القياسات التي تم إجراؤها في نظام إحداثي إلى آخر. على سبيل المثال، لنفترض أن ساعتك تسبق التوقيت القياسي المحلي بخمس دقائق. إذا كنت تعلم أن هذا هو الحال، فعندما يسألك شخص ما عن الوقت، يمكنك طرح خمس دقائق من الوقت المعروض على ساعتك للحصول على الوقت الصحيح. لذلك، فإن القياسات التي يجريها المراقب حول النظام تعتمد على الإطار المرجعي للمراقب (يمكنك القول أن الحافلة وصلت في الساعة الخامسة والثلاثة بينما وصلت بالفعل في الساعة الثالثة).

مثال إضافي (ما هو قانون القصور الذاتي) 

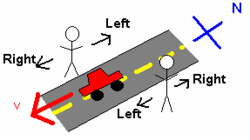
للحصول على مثال بسيط يتضمن فقط توجيه مراقبين اثنين، فكر في شخصين يقفان على جانبي شارع يمتد من الشمال إلى الجنوب. انظر الشكل 2. تمر بهم سيارة متجهة جنوبًا. بالنسبة للشخص الذي يواجه الشرق، كانت السيارة تتحرك إلى اليمين. ومع ذلك، بالنسبة للشخص الذي يواجه الغرب، كانت السيارة تتحرك إلى اليسار. يرجع هذا التناقض إلى أن هذين الشخصين استخدما إطارين مرجعيين مختلفين لفحص هذا النظام.

للحصول على مثال أكثر تعقيدًا يشتمل على مراقبين في حركة نسبية، فكر في ألفريد، الذي يقف على جانب الطريق ويراقب سيارة تمر به من اليسار إلى اليمين. في إطاره المرجعي، يحدد ألفريد النقطة التي يقف فيها على أنها نقطة الأصل، والطريق على أنها المحور السيني، والاتجاه المعاكس على أنه المحور الصادي الموجب. بالنسبة له، تتحرك السيارة على طول المحور x بسرعة معينة v في اتجاه x الموجب. يعتبر الإطار المرجعي لألفريد إطارًا مرجعيًا بالقصور الذاتي لأنه لا يتسارع (متجاهلاً التأثيرات مثل دوران الأرض والجاذبية).

الآن فكر في بيتسي، الشخص الذي يقود السيارة. تحدد بيتسي، عند اختيار إطارها المرجعي، موقعها على أنه الأصل، والاتجاه إلى يمينها باعتباره المحور السيني الموجب، والاتجاه المقابل لها باعتباره المحور الصادي الموجب. في هذا الإطار، كانت بيتسي ثابتة والعالم من حولها يتحرك – على سبيل المثال، عندما مرت بألفريد، لاحظته يتحرك بسرعة v في الاتجاه السلبي y. إذا كان يقود سيارته شمالًا، فإن الشمال هو الاتجاه الموجب لـ y. إذا اتجه نحو الشرق، يصبح الشرق هو الاتجاه الموجب y.

وأخيرًا، كمثال للمراقبين غير القصوريين، لنفترض أن كانديس تزيد من سرعة سيارتها. أثناء مروره بها، يقيس ألفريد تسارعها ويجدها في اتجاه x السالب. بافتراض أن تسارع كانديس ثابت، ما التسارع الذي تقيسه بيتسي؟ إذا كانت سرعة بيتسي v ثابتة، فهي في إطار مرجعي قصوري، وستجد التسارع في إطارها المرجعي، a في اتجاه y السالب، يساوي تسارع ألفريد. ومع ذلك، إذا تسارع بمعدل A في الاتجاه السلبي y a’ = a − A (بمعنى آخر، فإنه يقلل من تسارع كانديس)، فإن تسارع كانديس في الاتجاه السلبي y يكون مقدارًا أصغر من تسارع ألفريد . قياس. وبالمثل، إذا تسارع (تسارع) بمعدل A في اتجاه y الموجب، فإنه يلاحظ تسارع كانديس كـ a’ = a + A في اتجاه y السالب – وهي قيمة أكبر من قياس ألفريد.