اینرسی این ایده است که یک جسم به حرکت فعلی خود ادامه می دهد تا زمانی که نیرویی باعث شود سرعت یا جهت آن تغییر کند. این اصطلاح به درستی به عنوان کوتاه نویسی برای “اصل اینرسی” که توسط نیوتن در اولین قانون حرکتش توضیح داده شده است، درک می شود .
پس از تعاریف دیگر، نیوتن در اولین قانون حرکت خود می گوید:
قانون 1. هر جسمی در حالت سکون یا حرکت یکنواخت خود در یک خط راست استقامت می کند، مگر اینکه مجبور شود آن حالت را توسط نیروهایی که روی آن تأثیر می گذارد تغییر دهد.
کلمه “پشتکار” ترجمه مستقیم از لاتین نیوتن است. اصطلاحات کمتر دیگری مانند «ادامه دادن» یا «ماندن» معمولاً در کتابهای درسی مدرن یافت میشوند. استفاده مدرن از برخی تغییرات در مکانیک اصلی نیوتن (همانطور که در Principia بیان شد ) توسط اویلر ، دالامبر و دیگر دکارتی ها به وجود آمده است .
اصطلاح اینرسی از کلمه لاتین iners به معنای بیکار، تنبل گرفته شده است. اصطلاح اینرسی همچنین ممکن است به مقاومت هر جسم فیزیکی در برابر تغییر در سرعت آن اشاره کند . جسم است این شامل تغییرات در سرعت یا جهت حرکت . یکی از جنبه های این خاصیت تمایل اجسام به حرکت در یک خط مستقیم با سرعت ثابت در زمانی است که هیچ نیرویی بر آنها وارد نمی شود.
اینرسی یکی از مظاهر اولیه جرم است که از ویژگی های کمی سیستم های فیزیکی است .
تاریخی خود در فلسفه طبیعی ، Principia Mathematica ، اسحاق نیوتن اینرسی را به عنوان یک نیرو تعریف کرد:
تعریف III. vis insita یا نیروی ذاتی ماده، قدرت مقاومتی است که به وسیله آن هر جسمی، به همان اندازه که در آن نهفته است، تلاش میکند تا در وضعیت فعلی خود استقامت کند، خواه در حالت سکون یا حرکت یکنواخت به جلو در یک خط راست.
اصل اینرسی یکی از اصول اساسی در فیزیک کلاسیک است . امروزه نیز برای توصیف حرکت اجسام و چگونگی تأثیر نیروهای اعمال شده بر آنها بر آنها استفاده می شود.
تاریخچه و توسعه مفهوم
درک اولیه حرکت اینرسی
جان اچ. لینهارد اشاره می کند که موزی – بر اساس یک متن چینی از دوره کشورهای متخاصم (475-221 قبل از میلاد) – اولین توصیف اینرسی را ارائه کرده است. اروپا قبل از رنسانس ، نظریه رایج حرکت در فلسفه غرب نظریه ارسطو (335 قبل از میلاد تا 322 قبل از میلاد) بود. در سطح زمین، خاصیت اینرسی اجسام فیزیکی اغلب توسط گرانش و اثرات اصطکاک و مقاومت هوا پوشانده می شود ، که هر دو تمایل به کاهش سرعت اجسام متحرک (معمولاً تا نقطه سکون) دارند. فیلسوف این امر باعث شد که ارسطو معتقد شود که اجسام فقط تا زمانی که نیرو بر آنها اعمال شود حرکت می کنند. ارسطو گفت که تمام اجسام متحرک (روی زمین) در نهایت ساکن می شوند مگر اینکه نیروی خارجی (نیروی) به حرکت آنها ادامه دهد. ارسطو ادامه حرکت پرتابه ها را پس از جدا شدن از پروژکتورشان، به عنوان یک عمل (خود غیرقابل توضیح) از محیط اطراف که به حرکت دادن پرتابه ادامه می دهد، توضیح داد.
علیرغم پذیرش عمومی آن، مفهوم حرکت ارسطو در موارد متعددی توسط فیلسوفان برجسته طی نزدیک به دو هزار سال مورد مناقشه قرار گرفت . برای مثال، لوکرتیوس (احتمالاً به دنبال اپیکور ) اظهار داشت که «وضعیت پیشفرض» ماده حرکت است، نه سکون (رکود). در قرن ششم، جان فیلوپونوس از ناهماهنگی بین بحث ارسطو در مورد پرتابه ها، جایی که رسانه پرتابه ها را حفظ می کند، و بحث او در مورد فضای خالی، جایی که رسانه مانع حرکت جسم می شود، انتقاد کرد. فیلوپونوس پیشنهاد کرد که حرکت با عمل یک محیط اطراف حفظ نمی شود، بلکه توسط برخی از ویژگی هایی که در هنگام به حرکت در آمدن جسم به آن داده می شود. اگرچه این مفهوم مدرن اینرسی نبود، زیرا هنوز نیاز به نیرویی برای حفظ حرکت بدن وجود داشت، اما گامی اساسی در آن جهت ثابت کرد. این دیدگاه به شدت توسط Averroes و بسیاری از فیلسوفان مکتبی که از ارسطو حمایت کردند، مخالفت کردند. با این حال، این دیدگاه بدون چالش باقی نماند جهان اسلام ، جایی که فیلوپونوس حامیان متعددی داشت که افکار او را بیشتر توسعه دادند.
در قرن یازدهم، شاعر ایرانی ابن سینا (ابعلی سینا) ادعا کرد که پرتابه در خلاء متوقف نمی شود مگر اینکه به آن عمل شود.
نظریه انگیزه (قانون اینرسی چیست)
در قرن چهاردهم، ژان بوریدان این تصور را رد کرد که خاصیت مولد حرکت، که او آن را انگیزه نامید ، خود به خود از بین می رود. موضع بوریدان این بود که یک جسم متحرک با مقاومت هوا و وزن بدن که با نیروی محرکه آن مخالفت می کند، دستگیر می شود. بوریدان همچنین اظهار داشت که انگیزه با سرعت افزایش می یابد. بنابراین، ایده اولیه او از انگیزه از بسیاری جهات شبیه به مفهوم مدرن تکانه بود. علیرغم شباهتهای آشکار به ایدههای مدرنتر اینرسی، بوریدان نظریه خود را تنها اصلاحی در فلسفه اساسی ارسطو میدید، و بسیاری از دیدگاههای مشایی دیگر را حفظ میکرد ، از جمله این باور که هنوز تفاوتی اساسی بین یک جسم در حال حرکت و یک جسم در حال سکون وجود دارد. . بوریدان همچنین معتقد بود که انگیزه می تواند نه تنها خطی، بلکه دایره ای نیز باشد و باعث حرکت اجسام (مانند اجرام آسمانی) در یک دایره شود. نظریه بوریدان توسط شاگرد او آلبرت ساکسونی (1316-1390) و ماشین حساب های آکسفورد دنبال شد. او آزمایش های مختلفی انجام داد که مدل ارسطویی را بیشتر تضعیف کرد. کار آنها به نوبه خود توسط Nicole Oresme توضیح داده شد که پیشگام تمرین نشان دادن قوانین حرکت با نمودارها بود.
اندکی قبل از نظریه اینرسی گالیله، جیامباتیستا بندتی نظریه رو به رشد انگیزه را اصلاح کرد تا حرکت خطی را به تنهایی در بر گیرد:
«…[هر] بخشی از ماده مادی که وقتی انگیزهای توسط هر نیروی محرکهای بیرونی بر آن تأثیر گذاشته است، به خودی خود حرکت میکند، تمایل طبیعی به حرکت در مسیری مستقیم دارد، نه منحنی».
Benedetti حرکت یک سنگ در یک زنجیر را به عنوان نمونه ای از حرکت خطی ذاتی اجسام، که به حرکت دایره ای وادار می شود، ذکر می کند.
اینرسی کلاسیک
به گفته چارلز کولستون گیلیسپی ، اینرسی «به عنوان یک پیامد فیزیکی هندسی دکارت از ماده فضا، همراه با تغییرناپذیری خدا وارد علم شد». اولین فیزیکدانی که به طور کامل از مدل حرکت ارسطویی جدا شد، آیزاک بیکمن در سال 1614 بود. اصطلاح «اینرسی» برای اولین بار توسط یوهانس کپلر در Epitome Astronomiae Copernicanae (منتشر شده در سه بخش از) معرفی شد. 1617 تا 1621)؛ با این حال، معنای اصطلاح کپلر (که او از کلمه لاتین “تنبلی” یا “تنبلی” گرفته شده است) کاملاً با تفسیر مدرن آن یکی نبود. کپلر اینرسی را تنها بر حسب مقاومت در برابر حرکت تعریف کرد، یک بار دیگر بر اساس این پیش فرض که استراحت حالتی طبیعی است که نیازی به توضیح ندارد. تا زمانی که کار بعدی گالیله و نیوتن سکون و حرکت را در یک اصل متحد کرد که اصطلاح «اینرسی» را میتوان برای این مفاهیم به کار برد، همانطور که امروز است. اصل اینرسی، همانطور که ارسطو برای “حرکات در فضای خالی” فرموله کرد. [25] شامل این است که یک شی دنیوی تمایل به مقاومت در برابر تغییر در حرکت دارد. تقسیم ارسطویی حرکت به دنیایی و آسمانی در مواجهه با نتیجه گیری های نیکلاوس کوپرنیک در قرن شانزدهم، که معتقد بود زمین هرگز در حال استراحت نیست، در واقع در حرکت دائمی به دور خورشید است، به طور فزاینده ای مشکل ساز شد.

گالیله ، در توسعه بیشتر مدل کوپرنیک(قانون اینرسی چیست)
این مشکلات را با ماهیت پذیرفته شده حرکت در آن زمان تشخیص داد و در نتیجه، دست کم تا حدی، بیانی مجدد از توصیف ارسطو از حرکت در خلاء را به عنوان یک اصل فیزیکی اساسی گنجاند:
جسمی که روی یک سطح هموار حرکت می کند، در همان جهت با سرعت ثابت ادامه می دهد مگر اینکه دچار اختلال شود.
گالیله می نویسد که “همه موانع بیرونی برداشته شده، یک جسم سنگین بر روی یک سطح کروی متحدالمرکز با زمین، خود را در آن حالتی که در آن بوده است حفظ می کند؛ برای مثال، اگر در حرکتی به سمت غرب قرار گیرد، خود را در این حالت حفظ خواهد کرد. آن جنبش.” [27] این مفهوم، که توسط مورخان علم «اینرسی دایرهای» یا «اینرسی دایرهای افقی» نامیده میشود، پیش درآمدی برای مفهوم اینرسی مستطیلی نیوتن است، اما از آن متمایز است. [28] [29] برای گالیله، یک حرکت « افقی » است اگر جسم متحرک را به سمت مرکز زمین یا از آن دور نکند، و برای او، «مثلاً یک کشتی که یک بار نیروی محرکهای دریافت کرده است. دریای آرام، به طور مداوم در سراسر جهان ما بدون توقف حرکت می کند.” [30] [31] همچنین شایان ذکر است که گالیله بعداً (در سال 1632) به این نتیجه رسید که بر اساس این فرض اولیه اینرسی، تشخیص تفاوت بین یک جسم متحرک و یک جسم ساکن بدون اشاره خارجی برای مقایسه آن غیرممکن است. در برابر. [32] شد این مشاهدات در نهایت مبنایی برای آلبرت انیشتین تا نظریه نسبیت خاص را توسعه دهد .
او پالایش، اصلاح و مدون شد مفاهیم اینرسی در نوشتههای گالیله بعداً توسط اسحاق نیوتن به عنوان اولین قانون حرکت (برای اولین بار در اثر نیوتن، Philosophiæ Naturalis Principia Mathematica ، در سال 1687 منتشر شد):
هر جسمی در حالت سکون یا حرکت یکنواخت خود در یک خط راست استقامت می کند، مگر اینکه مجبور شود آن حالت را توسط نیروهایی که بر آن تأثیر می گذارد تغییر دهد.
با وجود اینکه نیوتن این مفهوم را به زیبایی در قوانین حرکت خود تعریف کرده بود، در واقع از اصطلاح “اینرسی” برای اشاره به قانون اول خود استفاده نکرد. در واقع، او در اصل پدیده مربوطه را ناشی از «نیروهای ذاتی» ذاتی ماده میدانست که در برابر هر شتابی مقاومت میکنند. با توجه به این دیدگاه و وام گرفتن از کپلر، نیوتن اصطلاح «اینرسی» را به معنای «نیروی ذاتی متعلق به جسمی که در برابر تغییرات در حرکت مقاومت میکند» نسبت داد. بنابراین، نیوتن «اینرسی» را به معنای علت پدیده تعریف کرد، نه خود پدیده. با این حال، ایده های اولیه نیوتن در مورد “نیروی مقاومتی ذاتی” در نهایت به دلایل مختلف مشکل ساز بود، و بنابراین اکثر فیزیکدانان دیگر با این شرایط فکر نمی کنند. از آنجایی که هیچ مکانیسم جایگزینی به آسانی پذیرفته نشده است، و اکنون به طور کلی پذیرفته شده است که ممکن است هیچ مکانیزمی وجود نداشته باشد که بتوانیم آن را بشناسیم، اصطلاح «اینرسی» به جای هر مکانیسم ذاتی، صرفاً به معنای خود پدیده است. بنابراین، در نهایت، “اینرسی” در فیزیک کلاسیک مدرن نامی برای همان پدیده ای است که توسط قانون اول حرکت نیوتن توصیف شده است، و این دو مفهوم اکنون معادل در نظر گرفته می شوند.
نسبیت
آلبرت انیشتین نظریه نسبیت خاص ، همانطور که در مقاله 1905 او با عنوان ” درباره الکترودینامیک اجسام متحرک ” ارائه شد، بر اساس درک چارچوب های مرجع اینرسی توسعه یافته توسط گالیله، هویگنس و نیوتن ساخته شد. در حالی که این نظریه انقلابی معنای بسیاری از مفاهیم نیوتنی مانند جرم ، انرژی و فاصله را به طور قابل توجهی تغییر داد ، مفهوم اینرسی انیشتین در ابتدا از معنای اصلی نیوتن بدون تغییر باقی ماند. با این حال، این منجر به یک محدودیت ذاتی در نسبیت خاص شد: اصل نسبیت فقط میتوانست برای چارچوبهای مرجع اینرسی اعمال شود. برای پرداختن به این محدودیت، انیشتین نظریه نسبیت عام خود را توسعه داد (“بنیاد نظریه نسبیت عام”، 1916)، که نظریه ای شامل غیر اینرسی چارچوب های مرجع (شتاب یافته) ارائه کرد.
در نسبیت عام، مفهوم حرکت اینرسی معنای وسیع تری پیدا کرد. با در نظر گرفتن نسبیت عام، حرکت اینرسی به هر حرکت جسمی گفته میشود که تحت تأثیر نیروهای الکتریکی، مغناطیسی یا منشاهای دیگر قرار نگیرد، بلکه تنها تحت تأثیر جرمهای گرانشی باشد. از نظر فیزیکی، این دقیقاً همان چیزی است که یک شتابسنج سه محوره تشخیص نمیدهد، نشان میدهد که به درستی کار میکند، زمانی که هیچ شتاب مناسبی را .
اینرسی چرخشی

اینرسی چرخشی
کمیت مربوط به اینرسی، اینرسی چرخشی (← گشتاور اینرسی ) است، این ویژگی که یک جسم صلب در حال چرخش حالت حرکت چرخشی یکنواخت خود را حفظ می کند . آن تکانه زاویه ای خارجی بدون تغییر باقی می ماند مگر اینکه یک گشتاور اعمال شود. به این بقای تکانه زاویه ای می گویند. اینرسی چرخشی اغلب در رابطه با یک جسم صلب در نظر گرفته می شود. به عنوان مثال، یک ژیروسکوپ از این خاصیت استفاده می کند که در برابر هرگونه تغییر در محور چرخش مقاومت می کند.
| بخشی از یک سریال در |
| مکانیک کلاسیک |
|---|
| اف = د د تی ( متر v ) قانون دوم حرکت |
|
شاخه ها |
مبانی |
فرمولاسیون |
موضوعات اصلی |
چرخش |
دانشمندان |
|
|
در فیزیک کلاسیک و نسبیت خاص ، یک اینرسی چارچوب مرجع (که به آن قاب مرجع اینرسی ، قاب اینرسی ، فضای اینرسی یا چارچوب مرجع گالیله نیز میگویند ) چارچوب مرجعی است که تحت هیچ شتابی قرار نمیگیرد . این چارچوبی است که در آن یک جسم فیزیکی ایزوله – جسمی با نیروی خالص صفر که بر آن وارد میشود – با سرعت ثابتی حرکت میکند (ممکن است سرعت صفر باشد) یا به طور معادل، چارچوب مرجعی است که در آن نیوتن قانون اول حرکت پابرجاست در حالت حرکت ثابت و مستطیلی همه فریم های اینرسی نسبت به یکدیگر هستند. به عبارت دیگر، یک شتاب سنج که با هر یک از آنها حرکت می کند، شتاب صفر را تشخیص می دهد.
مشاهده شده است که اجرام آسمانی که از اجرام دیگر دور هستند و با توجه به تابش پسزمینه مایکروویو کیهانی در حرکت یکنواخت هستند ، چنین حرکت یکنواختی را حفظ میکنند.
به اندازهگیری در دیگری تبدیل کرد اندازهگیریها در یک قاب اینرسی را میتوان با یک تبدیل ساده، تبدیل گالیله در فیزیک نیوتنی و تبدیل لورنتز در نسبیت خاص، .
در مکانیک تحلیلی ، چارچوب مرجع اینرسی را می توان به عنوان چارچوب مرجعی تعریف کرد که زمان و مکان را به صورت همگن ، همسانگرد و به روشی مستقل از زمان توصیف می کند.
در نسبیت عام
- در هر ناحیه ای که به اندازه کافی کوچک باشد که انحنای فضازمان و نیروهای جزر و مدی [5] ناچیز باشد، می توان مجموعه ای از قاب های اینرسی را یافت که تقریباً آن منطقه را توصیف می کنند.
- فیزیک یک سیستم [7] را می توان بر حسب یک قاب اینرسی بدون علل خارجی برای سیستم مربوطه توصیف کرد، به استثنای یک اثر ظاهری ناشی از جرم های به اصطلاح دور.
در یک قاب مرجع غیر اینرسی ، از دیدگاه فیزیک کلاسیک و نسبیت خاص، برهمکنشهای بین اجزای اساسی جهان قابل مشاهده (فیزیک یک سیستم ) بسته به شتاب آن قاب نسبت به یک قاب اینرسی متفاوت است. از این منظر و به دلیل پدیده اینرسی، نیروهای فیزیکی «معمول» بین دو جسم باید با نیروهای اینرسی ظاهراً بدون منبع تکمیل شوند . [9] [10] از دیدگاه نظریه نسبیت عام، نیروهای اینرسی ظاهری (علل خارجی تکمیلی) به حرکت ژئودزیکی در فضا-زمان نسبت داده می شود .
به عنوان مثال، در فیزیک کلاسیک، توپی که به سمت زمین رها می شود دقیقاً به سمت پایین حرکت نمی کند زیرا زمین در حال چرخش است. این بدان معناست که چارچوب مرجع یک ناظر روی زمین اینرسی نیست. در نتیجه علم فیزیک باید برای ، اثر کوریولیس – یک نیروی ظاهری – پیشبینی حرکت کوچک افقی مربوطه را در نظر بگیرد. مثال دیگری از نیروی ظاهری که در چارچوب های مرجع چرخان ظاهر می شود، مربوط به اثر گریز از مرکز ، نیروی گریز از مرکز است.
مجموعهای از فریمها که در آن قوانین فیزیک ساده هستند
حرکت یک جسم را فقط می توان نسبت به چیز دیگری توصیف کرد – اجسام دیگر، ناظران یا مجموعه ای از مختصات فضا-زمان. می گویند به این چارچوب های مرجع . اگر مختصات بد انتخاب شوند، قوانین حرکت ممکن است پیچیده تر از حد لازم به نظر برسند. به عنوان مثال، فرض کنید یک جسم آزاد که هیچ نیروی خارجی بر روی آن وارد نمی شود، در لحظه ای در حال استراحت است. در بسیاری از سیستم های مختصات، در لحظه بعدی شروع به حرکت می کند، حتی اگر هیچ نیرویی روی آن وجود نداشته باشد. با این حال، همیشه می توان یک چارچوب مرجع را انتخاب کرد که در آن ثابت بماند. به طور مشابه، اگر فضا به طور یکنواخت یا زمان به طور مستقل توصیف نشود، یک سیستم مختصات می تواند پرواز ساده یک جسم آزاد در فضا را به عنوان یک زیگزاگ پیچیده در سیستم مختصاتش توصیف کند. در واقع، خلاصهای بصری از قابهای اینرسی میتوان ارائه کرد: در یک قاب مرجع اینرسی، قوانین مکانیک سادهترین شکل خود را دارند.
طبق فرض اول نسبیت خاص ، همه قوانین فیزیکی سادهترین شکل خود را در یک قاب اینرسی به خود میگیرند و قابهای اینرسی متعددی وجود دارد که با ترجمه یکنواخت به هم مرتبط هستند :
اصل نسبیت خاص: اگر سیستمی از مختصات K به گونه ای انتخاب شود که در رابطه با آن، قوانین فیزیکی در ساده ترین شکل خود خوب باشند، همان قوانین در رابطه با هر سیستم دیگر مختصات K’ که با ترجمه یکنواخت نسبتاً حرکت می کنند، خوب هستند. به ک.
– آلبرت انیشتین: بنیاد نظریه نسبیت عام ، بخش A، §1
این سادگی خود را در این نشان می دهد که فریم های اینرسی دارای فیزیک مستقل و بدون نیاز به علل خارجی هستند، در حالی که فیزیک در قاب های غیر اینرسی دارای علل خارجی است. اصل سادگی را می توان در فیزیک نیوتنی و همچنین در نسبیت خاص استفاده کرد. به ناگل [12] و همچنین بلاگویویچ مراجعه کنید.
قوانین مکانیک نیوتنی همیشه به سادهترین شکل خود باقی نمیماند… اگر برای مثال، یک ناظر بر روی دیسکی قرار گیرد که نسبت به زمین میچرخد، نیرویی را حس میکند که او را به سمت حاشیه هل میدهد. از دیسک، که در اثر هیچ گونه تعامل با سایر اجسام ایجاد نمی شود. در اینجا، شتاب نتیجه نیروی معمول نیست، بلکه ناشی از نیروی به اصطلاح اینرسی است. قوانین نیوتن در ساده ترین شکل خود فقط در خانواده ای از چارچوب های مرجع به نام قاب های اینرسی وجود دارد. این واقعیت نشان دهنده ماهیت اصل نسبیت گالیله است:
قوانین مکانیک در تمام قاب های اینرسی یک شکل دارند.– میلوتین بلاگویویچ: گرانش و تقارن سنج ، ص 4
از نظر عملی، هم ارزی فریم های مرجع اینرسی به این معنی است که دانشمندان درون یک جعبه که به طور یکنواخت حرکت می کنند، نمی توانند سرعت مطلق خود را با هیچ آزمایشی تعیین کنند. در غیر این صورت، تفاوت ها یک چارچوب مرجع استاندارد مطلق ایجاد می کند. [14] [15] طبق این تعریف، که با ثبات سرعت نور تکمیل شده است، چارچوب های مرجع اینرسی در بین خود با توجه به تبدیل های تقارن پوانکره تغییر می کنند که تبدیل های لورنتس زیرگروهی از آن هستند. [16] در مکانیک نیوتنی، که می تواند به عنوان یک مورد محدود کننده نسبیت خاص در نظر گرفته شود که در آن سرعت نور بی نهایت است، چارچوب های مرجع اینرسی توسط گروه گالیله تقارن مرتبط هستند.
چارچوب مرجع اینرسی نیوتن
فضای مطلق
نیوتن فضای مطلقی را در نظر گرفت که به خوبی توسط یک چارچوب مرجع ثابت نسبت به ستارگان ثابت تقریب شده است . سپس یک قاب اینرسی نسبت به فضای مطلق ترجمه یکنواخت بود. با این حال، برخی از دانشمندان (که توسط ماخ «نسبیگرایان» نامیده میشوند ، حتی در زمان نیوتن، احساس کردند که فضای مطلق نقصی در فرمولبندی است و باید جایگزین شود.
در واقع، عبارت اینرسی مرجع ( به آلمانی : Inertialsystem در سال 1885 ابداع شد ) توسط لودویگ لانگ تا تعاریف نیوتن از «فضا و زمان مطلق» را با تعریف عملیاتیتر جایگزین کند . [18] [19] همانطور که توسط آیرو ترجمه شده است، لانگ تعریف زیر را ارائه کرد: [20]
قاب مرجعی که در آن یک نقطه جرمی که از یک نقطه در سه جهت مختلف (غیر همسطح) پرتاب می شود، هر بار که پرتاب می شود، مسیرهای مستقیم را دنبال می کند، قاب اینرسی نامیده می شود.
بحث در مورد پیشنهاد لانگ را می توان در ماخ یافت.
نارسایی مفهوم «فضای مطلق» در مکانیک نیوتنی توسط بلاگویویچ بیان شده است:
- وجود فضای مطلق با منطق درونی مکانیک کلاسیک در تضاد است، زیرا، طبق اصل نسبیت گالیله، هیچ یک از قاب های اینرسی را نمی توان جدا کرد.
- فضای مطلق نیروهای اینرسی را توضیح نمی دهد زیرا آنها با شتاب نسبت به هر یک از قاب های اینرسی مرتبط هستند.
- فضای مطلق بر روی اجسام فیزیکی با القای مقاومت آنها در برابر شتاب عمل می کند، اما نمی توان بر آن عمل کرد.
– میلوتین بلاگویویچ: گرانش و تقارن سنج ، ص 5
کاربرد تعاریف عملیاتی در نظریه نسبیت خاص بسیار بیشتر انجام شد. برخی پیشینه تاریخی از جمله تعریف لانگ توسط دیسال ارائه شده است که به طور خلاصه می گوید:
سوال اصلی، “قوانین حرکت نسبت به چه چارچوب مرجعی وجود دارد؟” آشکار می شود که به اشتباه مطرح شده است. زیرا قوانین حرکت اساساً یک کلاس از چارچوب های مرجع و (در اصل) روشی را برای ساخت آنها تعیین می کند.
– فضا و زمان رابرت دی سال : فریم های اینرسی
مکانیک نیوتنی
نظریههای کلاسیک که از تبدیل گالیله استفاده میکنند ، هم ارزی همه چارچوبهای مرجع اینرسی را فرض میکنند. برخی نظریه ها حتی ممکن است وجود یک چارچوب ممتاز را فرض کنند که فضای مطلق و زمان مطلق را فراهم می کند . تبدیل گالیله مختصات را از یک چارچوب مرجع اینرسی تبدیل می کند، س ، به دیگری، س ” با جمع یا تفریق ساده مختصات:
- r ” = r – r 0 – v تی
- تی ” = تی – تی 0
جایی که r 0 و t 0 نشان دهنده تغییرات در مبدأ فضا و زمان هستند و v سرعت نسبی دو قاب مرجع اینرسی است. تحت تبدیل های گالیله، زمان t 2 − t 1 بین دو رویداد برای همه فریم های مرجع یکسان است و فاصله بین دو رویداد همزمان (یا به طور معادل، طول هر جسم، | r 2 − r 1 |) نیز برابر است. یکسان.

در قلمرو مکانیک نیوتنی، چارچوب مرجع اینرسی یا چارچوب مرجع اینرسی، چارچوبی است که قانون اول حرکت نیوتن در آن معتبر است. [24] با این حال، اصل نسبیت خاص، مفهوم چارچوب اینرسی را تعمیم می دهد تا همه قوانین فیزیکی را شامل شود، نه فقط قانون اول نیوتن.
نیوتن قانون اول را در هر چارچوب مرجعی که در حرکت یکنواخت نسبت به ستارگان ثابت است معتبر میدانست. [25] یعنی نه در حال چرخش و نه شتاب نسبت به ستارگان. [26] امروزه مفهوم « فضای مطلق » کنار گذاشته شده است و یک قاب اینرسی در حوزه مکانیک کلاسیک به این صورت تعریف میشود: [27] [28]
چارچوب مرجع اینرسی، چارچوبی است که در آن حرکت ذره ای که تحت تأثیر نیرو قرار نمی گیرد، در یک خط مستقیم با سرعت ثابت باشد.
بنابراین، با توجه به یک قاب اینرسی، یک جسم یا جسم شتاب می گیرد تنها زمانی که نیروی فیزیکی اعمال شود، و (به پیروی از قانون اول حرکت نیوتن )، در غیاب نیروی خالص، جسم در حال سکون در حالت سکون باقی می ماند و بدن در حال حرکت به حرکت یکنواخت ادامه خواهد داد، یعنی در یک خط مستقیم و با سرعت ثابت . بین یکدیگر تغییر شکل می دهند قاب های اینرسی نیوتنی با توجه به گروه تقارن گالیله ای .
اگر این قانون به این صورت تفسیر شود که حرکت خط مستقیم نشان دهنده نیروی خالص صفر است، قاعده قاب های مرجع اینرسی را شناسایی نمی کند زیرا حرکت خط مستقیم را می توان در انواع قاب ها مشاهده کرد. اگر قانون به عنوان تعریف یک قاب اینرسی تفسیر شود، باید بتوانیم تعیین کنیم که چه زمانی نیروی خالص صفر اعمال می شود. این مشکل توسط اینشتین خلاصه شد: [29]
ضعف اصل اینرسی در این است که شامل استدلال در یک دایره است: جرمی بدون شتاب حرکت می کند اگر به اندازه کافی از اجسام دیگر دور باشد. ما می دانیم که به اندازه کافی از اجسام دیگر فاصله دارد تنها به این دلیل که بدون شتاب حرکت می کند.
— آلبرت انیشتین: معنای نسبیت ، ص. 58
چندین رویکرد برای این موضوع وجود دارد. یک رویکرد این است که استدلال کنیم که همه نیروهای واقعی با فاصله از منابع خود به روشی شناخته شده کاهش می یابند، بنابراین ما فقط باید مطمئن باشیم که جسم به اندازه کافی از همه منابع دور است تا اطمینان حاصل شود که هیچ نیرویی وجود ندارد. [30] یکی از مسائل احتمالی در این رویکرد، دیدگاه دیرینه تاریخی است که جهان دور ممکن است بر مسائل تأثیر بگذارد ( اصل ماخ ). رویکرد دیگر این است که همه منابع واقعی برای نیروهای واقعی شناسایی و آنها را محاسبه کنیم. یک مشکل احتمالی در این رویکرد این است که ما ممکن است چیزی را از دست بدهیم، یا شاید دوباره به دلیل اصل ماخ و درک ناقص جهان، تأثیر آنها را به طور نامناسبی در نظر بگیریم. رویکرد سوم این است که به نحوه تغییر نیروها در هنگام تغییر چارچوب های مرجع نگاه کنیم. نیروهای ساختگی، آنهایی که در اثر شتاب یک فریم به وجود می آیند، در قاب های اینرسی ناپدید می شوند و در موارد کلی قوانین پیچیده تبدیل دارند. بر اساس جهانی بودن قانون فیزیکی و درخواست چارچوب هایی که قوانین در آنها به سادگی بیان می شوند، چارچوب های اینرسی با فقدان چنین نیروهای ساختگی متمایز می شوند.
نیوتن اصل نسبیت را خود در یکی از پیامدهای خود به قوانین حرکت بیان کرد: [31] [32]
حرکات اجسام موجود در یک فضای معین بین خودشان یکسان است، خواه آن فضا در حالت سکون باشد یا به طور یکنواخت در یک خط مستقیم به جلو حرکت کند.
– اسحاق نیوتن: اصول ، نتیجه پنجم، ص. 88 در ترجمه اندرو موته
این اصل از دو جهت با اصل خاص متفاوت است : اول اینکه منحصر به مکانیک است و دوم اینکه هیچ اشاره ای به سادگی نمی کند. این اصل خاص را در تغییر ناپذیری شکل توصیف در میان چارچوب های مرجع متقابل ترجمه می کند. [33] نقش نیروهای ساختگی در طبقه بندی چارچوب های مرجع در ادامه بیشتر دنبال می شود.
اظهارات
مهم است که به برخی از مفروضات مطرح شده در بالا در مورد چارچوب های مختلف اینرسی مرجع توجه کنید. به عنوان مثال، نیوتن از زمان جهانی استفاده کرد، همانطور که در مثال زیر توضیح داده شده است. فرض کنید شما صاحب دو ساعت هستید که هر دو دقیقاً با یک نرخ تیک می زنند. شما آنها را همگام می کنید تا هر دو دقیقاً در یک زمان نمایش داده شوند. اکنون دو ساعت از هم جدا شدهاند و یکی از ساعتها در قطاری در حال حرکت است که با سرعت ثابت به سمت دیگری حرکت میکند. به گفته نیوتن، این دو ساعت همچنان با یک سرعت تیک تاک خواهند کرد و هر دو زمان یکسانی را نشان خواهند داد. نیوتن می گوید (قانون اینرسی چیست) که سرعت زمان اندازه گیری شده در یک چارچوب مرجع باید با نرخ زمان در دیگری یکسان باشد. به این معنا که یک زمان «جهانی» وجود دارد و همه زمانهای دیگر در همه چارچوبهای مرجع دیگر بدون توجه به موقعیت و سرعتشان با همان سرعت زمان جهانی اجرا میشوند. این مفهوم زمان و همزمانی بعداً توسط انیشتین در نظریه نسبیت خاص خود تعمیم یافت (1905) جایی که او دگرگونی هایی را بین چارچوب های مرجع اینرسی بر اساس ماهیت جهانی قوانین فیزیکی و اقتصاد بیان آنها ایجاد کرد. تحولات لورنتس ).
قاب های مرجع به ویژه در نسبیت خاص مهم هستند، زیرا وقتی یک قاب مرجع با کسری قابل توجهی از سرعت نور حرکت می کند، جریان زمان در آن قاب لزوماً در قاب دیگری اعمال نمی شود. سرعت نور تنها ثابت واقعی بین فریم های مرجع متحرک در نظر گرفته می شود.
تعریف چارچوب مرجع اینرسی را می توان فراتر از فضای اقلیدسی سه بعدی نیز گسترش داد. نیوتن فضای اقلیدسی را فرض کرد، اما نسبیت عام از هندسه عمومی تری استفاده می کند. به عنوان مثالی از اهمیت این موضوع، هندسه یک بیضی را در نظر بگیرید. در این هندسه، یک ذره “آزاد” به عنوان ذره ای در حال استراحت یا حرکت با سرعت ثابت در یک ژئودزیکی مسیر تعریف می شود. دو ذره آزاد ممکن است از یک نقطه روی سطح شروع شوند و با سرعت ثابت یکسانی در جهات مختلف حرکت کنند. پس از مدتی، این دو ذره در طرف مقابل بیضی با هم برخورد می کنند. هر دو ذره “آزاد” با سرعت ثابتی حرکت می کردند و این تعریف را برآورده می کردند که هیچ نیرویی عمل نمی کند. هیچ شتابی رخ نداد و بنابراین قانون اول نیوتن درست بود. این بدان معنی است که ذرات در چارچوب مرجع اینرسی بودند. از آنجایی که هیچ نیرویی عمل نمی کرد، هندسه موقعیت بود که باعث شد این دو ذره دوباره یکدیگر را ملاقات کنند. به روشی مشابه، اکنون توصیف آن رایج است [34] که ما در یک هندسه چهار بعدی به نام فضازمان وجود داریم . در این تصویر، انحنای این فضای چهاربعدی مسئول نحوهای است که در آن دو جسم با جرم به هم نزدیک میشوند، حتی اگر هیچ نیرویی عمل نکند. این انحنای فضازمان جایگزین نیرویی می شود که در مکانیک نیوتنی و نسبیت خاص به عنوان گرانش شناخته می شود.
نسبیت خاص(قانون اینرسی چیست)
اینشتین نظریه نسبیت خاص ، مانند مکانیک نیوتنی، هم ارزی همه چارچوب های مرجع اینرسی را فرض می کند. با این حال، از آنجا که نسبیت خاص فرض می کند که سرعت نور در فضای آزاد است ثابت ، تبدیل بین قاب های اینرسی تبدیل لورنتز است ، نه تبدیل گالیله که در مکانیک نیوتنی استفاده می شود. تغییرناپذیری سرعت نور منجر به پدیده های غیر شهودی مانند اتساع زمان و انقباض طول و نسبیت همزمانی می شود که به طور گسترده به صورت تجربی تأیید شده اند. [35] با نزدیک شدن سرعت نور به بی نهایت یا با نزدیک شدن سرعت نسبی بین فریم ها به صفر، تبدیل لورنتس به تبدیل گالیله ای کاهش می یابد. [36]
فریم های غیر اینرسی
در اینجا رابطه بین چارچوب های مرجع مشاهده ای اینرسی و غیر اینرسی در نظر گرفته می شود. تفاوت اساسی بین این قاب ها نیاز به قاب های غیر اینرسی به نیروهای ساختگی است که در زیر توضیح داده شده است.
نسبیت عام
نسبیت عام مبتنی بر اصل هم ارزی است:
هیچ آزمایشی وجود ندارد که ناظران بتوانند تشخیص دهند که آیا یک شتاب به دلیل نیروی گرانشی ایجاد می شود یا به دلیل اینکه چارچوب مرجع آنها در حال شتاب است.
— داگلاس سی جیانکولی، فیزیک برای دانشمندان و مهندسان با فیزیک مدرن ، ص. 155.
این ایده در مقاله انیشتین در سال 1907 با عنوان “اصل نسبیت و گرانش” معرفی شد و بعداً در سال 1911 توسعه یافت. یافت می شود پشتیبانی از این اصل در آزمایش Eötvös ، که تعیین می کند آیا نسبت جرم اینرسی به جرم گرانشی برای همه یکسان است یا خیر. بدن بدون در نظر گرفتن اندازه یا ترکیب. تا به امروز هیچ تفاوتی در چند قسمت در 10 11 یافت نشده است. برای برخی از بحثها در مورد ظرافتهای آزمایش Eötvös، مانند توزیع جرم محلی در اطراف محل آزمایش (از جمله کنایهای در مورد جرم Eötvös خود)، به فرانکلین مراجعه کنید.
اینشتین نظریه عمومی تمایز بین اثرات اسمی “اینرسی” و “غیر اینرسی” را با جایگزینی فضای “مسطح” مینکوفسکی نسبیت خاص با متریکی که انحنای غیر صفر ایجاد می کند، اصلاح می کند. در نسبیت عام، اصل اینرسی با اصل حرکت ژئودزیکی جایگزین می شود ، به موجب آن اجسام به روشی که انحنای فضازمان دیکته می شود حرکت می کنند. در نتیجه این انحنا، در نسبیت عام مشخص نیست که اجسام اینرسی که با سرعت خاصی نسبت به یکدیگر حرکت می کنند، به این حرکت ادامه دهند. این پدیده انحراف ژئودزیکی به این معنی است که چارچوب های مرجع اینرسی در سطح جهانی مانند مکانیک نیوتنی و نسبیت خاص وجود ندارد.
با این حال، نظریه عمومی در مناطق به اندازه کافی کوچک از فضازمان به نظریه خاص تقلیل می یابد، جایی که اثرات انحنای اهمیت کمتری پیدا می کند و آرگومان های قاب اینرسی اولیه می توانند دوباره وارد بازی شوند. در نتیجه، نسبیت خاص مدرن اکنون فقط به عنوان یک “نظریه محلی” توصیف می شود. “محلی” می تواند، برای مثال، کل کهکشان راه شیری را در بر گیرد: کارل شوارتزشیلد ، ستاره شناس ، حرکت جفت ستاره هایی را که به دور یکدیگر می چرخند، مشاهده کرد. او دریافت که دو مدار ستارگان چنین منظومهای در یک صفحه قرار دارند و حضیض مدارهای دو ستاره نسبت به منظومه شمسی در یک جهت است. شوارتزشیلد خاطرنشان کرد که این موضوع همیشه دیده میشود: جهت حرکت زاویهای تمام منظومههای ستارهای دوگانه مشاهدهشده نسبت به جهت حرکت زاویهای منظومه شمسی ثابت میماند. این مشاهدات به او این امکان را داد که به این نتیجه برسد که چارچوب های اینرسی درون کهکشان نسبت به یکدیگر نمی چرخند و فضای راه شیری تقریباً گالیله ای یا مینکوفسکی است.
فریم های اینرسی و چرخش (قانون اینرسی چیست)
در یک چارچوب اینرسی، قانون اول نیوتن ، قانون اینرسی ، برآورده می شود: هر حرکت آزاد دارای یک مقدار و جهت ثابت است. قانون دوم نیوتن برای یک ذره به شکل زیر است:
- اف = متر آ ،
با F نیروی خالص ( بردار )، ذره ( همچنین یک m جرم یک ذره و a شتاب بردار) که توسط یک ناظر در حالت سکون در قاب اندازه گیری می شود. نیروی F تمام نیروهای «واقعی» روی ذره است مجموع برداری ، مانند نیروهای تماسی ، الکترومغناطیسی، گرانشی و نیروهای هسته ای.
در مقابل، قانون دوم نیوتن در یک چارچوب مرجع دوار (یک چارچوب مرجع غیر اینرسی )، که با سرعت زاویهای Ω حول یک محور میچرخد، به شکل زیر است:
- اف ” = متر آ ،
که مانند یک قاب اینرسی به نظر می رسد، اما اکنون نیروی F ‘ حاصل نه تنها F بلکه عبارت های اضافی است (بند بعدی این معادله نکات اصلی را بدون ریاضیات دقیق ارائه می دهد):
- اف ” = اف – 2 متر اوه × v ب – متر اوه × ( اوه × ایکس ب ) – متر د اوه د تی × ایکس ب ،
در جایی که چرخش زاویهای کادر با بردار Ω نشان داده میشود که در جهت محور چرخش است، و با بزرگی برابر با نرخ زاویهای چرخش Ω ، نماد × نشاندهنده حاصلضرب بردار است ، بردار x B بدنه را نشان میدهد و بردار v B است سرعت جسم با توجه به یک ناظر دوار (متفاوت از سرعت مشاهده شده توسط ناظر اینرسی).
اصطلاحات اضافی در نیروی F “نیروهای “ساختگی” برای این قاب هستند که علل آنها خارج از سیستم در قاب است. اولین عبارت اضافی نیروی کوریولیس , دومی نیروی گریز از مرکز و سومی نیروی اویلر است . این عبارات همگی این ویژگی ها را دارند: وقتی Ω = 0 ناپدید می شوند. یعنی برای یک قاب اینرسی (که البته نمی چرخد) صفر هستند. آنها بسته به مقدار خاص Ω در هر قاب چرخشی، مقدار و جهت متفاوتی به خود می گیرند . آنها در قاب چرخان همه جا وجود دارند (بر هر ذره، صرف نظر از شرایط، تأثیر می گذارند). ندارند و هیچ منبع آشکاری در منابع فیزیکی قابل شناسایی به ویژه ماده . همچنین، نیروهای ساختگی با فاصله از بین نمی روند (برخلاف، برای مثال، نیروهای هسته ای یا نیروهای الکتریکی ). به عنوان مثال، نیروی گریز از مرکز که به نظر می رسد از محور چرخش در یک قاب دوار خارج می شود، با فاصله از محور افزایش می یابد.
همه ناظران در مورد نیروهای واقعی اتفاق نظر دارند F. ، فقط ناظران غیر اینرسی به نیروهای ساختگی نیاز دارند. قوانین فیزیک در قاب اینرسی ساده تر هستند زیرا نیروهای غیر ضروری وجود ندارند.
در زمان نیوتن، ستارگان ثابت به عنوان یک چارچوب مرجع، ظاهراً در حالت سکون نسبت به فضای مطلق، فراخوانی می شدند . در چارچوب های مرجعی که یا نسبت به ستارگان ثابت در حالت سکون بودند یا در ترجمه یکنواخت نسبت به این ستارگان، قوانین حرکت نیوتن وجود داشت. در مقابل، در قابهایی که نسبت به ستارههای ثابت شتاب میگیرند، که یکی از موارد مهم قابهایی است که نسبت به ستارههای ثابت میچرخند، قوانین حرکت در سادهترین شکل خود باقی نمیماند، بلکه باید با افزودن نیروهای ساختگی تکمیل میشد . به عنوان مثال، نیروی کوریولیس و نیروی گریز از مرکز . دو آزمایش توسط نیوتن ابداع شد تا نشان دهد چگونه می توان این نیروها را کشف کرد و بدین ترتیب به ناظر نشان داد که آنها در یک چارچوب اینرسی نیستند: مثال کشش در بند ناف که دو کره را که به دور مرکز ثقل خود می چرخند، و مثال . انحنای سطح آب در یک سطل دوار . در هر دو مورد، اعمال قانون دوم نیوتن برای مشاهده گر دوار بدون احضار نیروهای گریز از مرکز و کوریولیس برای توضیح مشاهدات آنها کار نمی کند (کشش در مورد کره ها، سطح آب سهموی در مورد سطل دوار).
همانطور که اکنون می دانیم، ستاره های ثابت ثابت نیستند. آنهایی که در کهکشان راه شیری زندگی می کنند با کهکشان می چرخند و حرکات مناسبی از خود نشان می دهند . آنهایی که خارج از کهکشان ما هستند (مانند سحابی هایی که زمانی به اشتباه ستاره بودند) در حرکت خود نیز شرکت می کنند، تا حدی به دلیل انبساط کیهان ، و بخشی به دلیل سرعت های عجیب و غریب . [46] برای مثال، کهکشان آندرومدا است در مسیر برخورد با کهکشان راه شیری با سرعت 117 کیلومتر بر ثانیه. مفهوم چارچوب های مرجع اینرسی دیگر نه به ستاره های ثابت و نه به فضای مطلق گره خورده است. بلکه شناسایی یک قاب اینرسی بر اساس سادگی قوانین فیزیک در قاب است. جان استاچل نوشت: زمانی که از وجود یک چارچوب مرجع ممتاز (قاب اتر) دست کشید، دلیلی وجود نداشت که در نسبیت فریم های اینرسی متوقف شود. پاسخ متعارف به چنین شبهاتی این بود که قوانین طبیعت در چارچوب های مرجع اینرسی شکل ساده تری به خود می گیرند زیرا در این چارچوب ها هنگام نوشتن قانون حرکت نیوتن نیازی به معرفی نیروهای اینرسی نیست.
در عمل، اگرچه الزامی نیست، استفاده از یک چارچوب مرجع مبتنی بر ستارگان ثابت بهگونهای که گویی یک چارچوب مرجع اینرسی است، اختلاف بسیار کمی را ایجاد میکند. به عنوان مثال، شتاب گریز از مرکز زمین به دلیل چرخش آن به دور خورشید حدود 30 میلیون برابر بیشتر از شتاب خورشید در مرکز کهکشان است.
برای توضیح بیشتر، این سوال را در نظر بگیرید: “آیا جهان ما می چرخد؟” برای پاسخ، ممکن است سعی کنیم شکل کهکشان راه شیری را با استفاده از قوانین فیزیک توضیح دهیم، [50] اگرچه مشاهدات دیگر ممکن است قطعی تر باشند. یعنی اختلافات بزرگتر یا عدم قطعیت اندازهگیری کمتر ، مانند ناهمسانگردی تابش پسزمینه مایکروویو یا سنتز هستهای بیگ بنگ. مسطح بودن کهکشان راه شیری به سرعت چرخش آن در یک چارچوب مرجع اینرسی بستگی دارد. اگر سرعت ظاهری چرخش آن را کاملاً به چرخش در یک قاب اینرسی نسبت دهیم، «صافی» متفاوتی پیشبینی میشود تا اینکه فرض کنیم بخشی از این چرخش در واقع ناشی از چرخش جهان است و نباید در چرخش کهکشان لحاظ شود. خود بر اساس قوانین فیزیک، مدلی تنظیم شده است که در آن یک پارامتر سرعت چرخش کیهان است. اگر قوانین فیزیک با مشاهدات در یک مدل با چرخش بیشتر از بدون آن موافق باشد، ما تمایل داریم بهترین مقدار را برای چرخش انتخاب کنیم، مشروط به سایر مشاهدات تجربی مرتبط. اگر هیچ مقداری از پارامتر چرخش موفقیت آمیز نباشد و تئوری در خطای مشاهده ای نباشد، اصلاح قانون فیزیکی در نظر گرفته می شود، برای مثال، ماده تاریک برای توضیح منحنی چرخش کهکشانی فراخوانی می شود . تا کنون، مشاهدات نشان میدهند که هر چرخشی در جهان بسیار آهسته است، نه سریعتر از یک بار در هر 6 × 10 13 سال (10-13 راد در سال)، وجود دارد یا خیر و بحث در مورد اینکه آیا چرخشی ادامه دارد. با این حال، اگر چرخش یافت می شد، تفسیر مشاهدات در چارچوبی که به کیهان گره خورده است باید برای نیروهای ساختگی موجود در چنین چرخشی در فیزیک کلاسیک و نسبیت خاص تصحیح شود، یا به عنوان انحنای فضازمان و حرکت ماده در طول تعبیر شود. ژئودزیک در نسبیت عام
وقتی اثرات کوانتومی مهم هستند، پیچیدگیهای مفهومی دیگری نیز در چارچوبهای مرجع کوانتومی به وجود میآیند .
قاب های پرایم شده (قانون اینرسی چیست)
یک قاب مرجع شتابدار اغلب بهعنوان قاب «پرده» مشخص میشود و همه متغیرهایی که به آن فریم وابسته هستند با اعداد اول نشانداده میشوند، بهعنوان مثال x’ , y’ , a’ .
بردار از مبدا یک قاب مرجع اینرسی تا مبدا یک قاب مرجع شتابدار معمولاً با R نشان داده میشود . با توجه به نقطه مورد علاقه ای که در هر دو فریم وجود دارد، بردار از مبدأ اینرسی به نقطه را r و بردار از مبدا شتاب گرفته تا نقطه را r’ می نامند . از هندسه موقعیت به دست می آوریم
- r = آر + r ” .
با در نظر گرفتن مشتقات اول و دوم از این با توجه به زمان، به دست می آوریم
- v = V + v ” ،
- آ = آ + آ ” .
که در آن V و A سرعت و شتاب سیستم شتاب نسبت به سیستم اینرسی و v و a سرعت و شتاب نقطه مورد نظر نسبت به قاب اینرسی هستند.
این معادلات امکان تبدیل بین دو سیستم مختصات را فراهم می کند. برای مثال، اکنون میتوانیم قانون دوم نیوتن را بنویسیم
- اف = متر آ = متر آ + متر آ ” .
هنگامی که حرکت شتاب گرفته به دلیل نیرویی که اعمال می شود، تجلی اینرسی است. اگر یک خودروی الکتریکی که برای شارژ مجدد سیستم باتری خود در هنگام کاهش سرعت طراحی شده است، به ترمز تبدیل شود، باتری ها دوباره شارژ می شوند که نشان دهنده قدرت فیزیکی تجلی اینرسی است. با این حال، تجلی اینرسی مانع از شتاب (یا کاهش سرعت) نمی شود، زیرا تجلی اینرسی در پاسخ به تغییر سرعت در اثر یک نیرو رخ می دهد. از منظر یک چارچوب چرخشی مرجع، تجلی اینرسی به نظر می رسد که نیرویی را اعمال می کند (یا در جهت گریز از مرکز ، یا در جهت متعامد به حرکت یک جسم، اثر کوریولیس ).
یک نوع رایج از قاب مرجع شتابدار، فریمی است که هم در حال چرخش و هم در حال ترجمه است (مثلاً یک فریم مرجع متصل به یک CD است که در حین حمل پخشکننده در حال پخش است). این ترتیب به معادله منتهی می شود ( نیروی ساختگی برای یک مشتق را ببینید):
- آ = آ ” + اوه ˙ × r ” + 2 اوه × v ” + اوه × ( اوه × r ” ) + آ 0 ،
یا، برای حل شتاب در قاب شتاب،
- آ ” = آ – اوه ˙ × r ” – 2 اوه × v ” – اوه × ( اوه × r ” ) – آ 0 .
ضرب در جرم m به دست می آید
- اف ” = اف پ ساعت y س من ج آ ل + اف E تو ل ه r ” + اف سی o r من o ل من س ” + اف ج ه n تی r من پ ه تی آ ل ” – متر آ 0 ،
جایی که
- اف E تو ل ه r ” = – متر اوه ˙ × r ” ( نیروی اویلر )
- اف سی o r من o ل من س ” = – 2 متر اوه × v ” ( نیروی کوریولیس )،
- اف ج ه n تی r من f تو g آ ل ” = – متر اوه × ( اوه × r ” ) = متر ( اوه 2 r ” – ( اوه ⋅ r ” ) اوه ) ( نیروی گریز از مرکز ).
جداسازی فریم های مرجع غیر اینرسی از اینرسی
نظریه


قاب های مرجع اینرسی و غیر اینرسی را می توان با عدم وجود یا حضور نیروهای ساختگی همانطور که به اختصار توضیح داده شد، تشخیص داد. [9] [10]
تأثیر این وجود در قاب غیر اینرسی این است که ناظر را ملزم به وارد کردن نیروی ساختگی به محاسبات خود می کند.
– سیدنی بوروویتز و لارنس بورنشتاین در دیدگاهی معاصر از فیزیک ابتدایی ، ص. 138
وجود نیروهای ساختگی نشان میدهد که قوانین فیزیکی سادهترین قوانین موجود نیستند، بنابراین، از نظر اصل نسبیت خاص ، چارچوبی که در آن نیروهای ساختگی وجود دارند، چارچوب اینرسی نیست:
معادلات حرکت در یک سیستم غیر اینرسی با معادلات یک سیستم اینرسی با اصطلاحات اضافی به نام نیروهای اینرسی متفاوت است. این به ما اجازه می دهد تا ماهیت غیر اینرسی یک سیستم را به طور تجربی تشخیص دهیم.
— VI Arnol’d: Mathematical Methods of Classical Mechanics ویرایش دوم، ص. 129
اجسام در چارچوب های مرجع غیر اینرسی در معرض نیروهای به اصطلاح ساختگی (نیروهای شبه) هستند. یعنی نیروهایی که ناشی از شتاب خود چارچوب مرجع هستند و نه از نیروی فیزیکی وارد بر بدن. نمونه هایی از نیروهای ساختگی عبارتند از نیروی گریز از مرکز و نیروی کوریولیس در چارچوب های مرجع چرخان .
پس چگونه می توان نیروهای «ساختگی» را از نیروهای «واقعی» جدا کرد؟ به کار بردن تعریف نیوتنی از قاب اینرسی بدون این جداسازی دشوار است. به عنوان مثال، یک جسم ثابت را در یک قاب اینرسی در نظر بگیرید. در حالت استراحت، هیچ نیروی خالصی اعمال نمی شود. اما در یک قاب که حول یک محور ثابت میچرخد، به نظر میرسد که جسم به صورت دایرهای حرکت میکند و تحت نیروی مرکزگرا (که از نیروی کوریولیس و نیروی گریز از مرکز تشکیل شده است) قرار میگیرد. چگونه می توانیم تصمیم بگیریم که قاب چرخان یک قاب غیر اینرسی است؟ دو رویکرد برای این قطعنامه وجود دارد: یک رویکرد این است که منشا نیروهای ساختگی (نیروی کوریولیس و نیروی گریز از مرکز) را جستجو کنیم. ما متوجه خواهیم شد که هیچ منبعی برای این نیروها وجود ندارد، هیچ حامل نیروی مرتبط ، هیچ بدن مبدأ وجود ندارد. [56] رویکرد دوم، نگاه به انواع چارچوب های مرجع است. برای هر قاب اینرسی، نیروی کوریولیس و نیروی گریز از مرکز ناپدید میشوند، بنابراین استفاده از اصل نسبیت خاص این قابها را که در آن نیروها ناپدید میشوند، بهعنوان مشترک و سادهترین قوانین فیزیکی شناسایی میکند و از این رو حکم میکند که قاب چرخان یک قاب چرخان نیست. قاب اینرسی
نیوتن خودش این مشکل را با استفاده از کرههای دوار بررسی کرد، همانطور که در شکل 2 و شکل 3 نشان داده شده است. او اشاره کرد که اگر کرهها نچرخند، کشش در رشته پیوند در هر چارچوب مرجع صفر اندازهگیری میشود. [57] اگر کرهها فقط در حال چرخش به نظر میرسند (یعنی ما کرههای ساکن را از یک قاب چرخان تماشا میکنیم)، کشش صفر در ریسمان با مشاهده اینکه نیروی گریز از مرکز توسط نیروهای گریز از مرکز و کوریولیس به صورت ترکیبی تأمین میشود، محاسبه میشود. ، بنابراین نیازی به تنش نیست. اگر کره ها واقعاً در حال چرخش باشند، کشش مشاهده شده دقیقاً همان نیروی مرکزگرای مورد نیاز حرکت دایره ای است. بنابراین، اندازهگیری کشش در رشته، قاب اینرسی را مشخص میکند: این کادری است که در آن کشش در رشته دقیقاً نیروی مرکزگرای مورد نیاز حرکت را همانطور که در آن قاب مشاهده میشود، فراهم میکند، و نه مقدار متفاوتی. یعنی قاب اینرسی همان چارچوبی است که در آن نیروهای ساختگی ناپدید می شوند.
اینقدر برای نیروهای ساختگی ناشی از چرخش. با این حال، برای شتاب خطی ، نیوتن ایده غیرقابل کشف شتاب های خط مستقیم مشترک را بیان کرد: [32]
اگر اجسام، به هر نحوی که بین خود حرکت می کنند، در جهت خطوط موازی توسط نیروهای شتاب دهنده مساوی به حرکت درآیند، به حرکت خود در بین خود ادامه می دهند، به همان شیوه ای که گویی هیچ نیرویی به آنها اغراق نکرده است.
– اسحاق نیوتن: نتیجه گیری اصل ششم، ص. 89، در ترجمه اندرو موته
این اصل مفهوم قاب اینرسی را تعمیم می دهد. به عنوان مثال، ناظری که در یک بالابر سقوط آزاد محصور شده است، ادعا می کند که خودش یک قاب اینرسی معتبر است، حتی اگر تحت نیروی گرانش در حال شتاب گرفتن باشد، تا زمانی که در مورد چیزی خارج از بالابر اطلاعاتی نداشته باشد. بنابراین، به طور دقیق، قاب اینرسی یک مفهوم نسبی است. با در نظر گرفتن این موضوع، میتوان قابهای اینرسی را مجموعاً مجموعهای از قابها تعریف کرد که نسبت به یکدیگر ثابت یا با سرعت ثابت حرکت میکنند، به طوری که یک قاب اینرسی به عنوان عنصری از این مجموعه تعریف میشود.
برای اعمال این ایدهها، هر چیزی که در قاب مشاهده میشود باید تابع یک خط مبنا و شتاب مشترک باشد که توسط خود فریم مشترک است. این وضعیت، به عنوان مثال، در مورد مثال آسانسور، که در آن همه اجرام در معرض شتاب گرانشی یکسانی هستند، و خود آسانسور با سرعت یکسانی شتاب میگیرد، صدق میکند.
برنامه های کاربردی (قانون اینرسی چیست)
سیستمهای ناوبری اینرسی از خوشهای از ژیروسکوپ و شتابسنج برای تعیین شتابهای نسبت به فضای اینرسی استفاده کردند. پس از چرخاندن یک ژیروسکوپ در یک جهت خاص در فضای اینرسی، قانون بقای تکانه زاویه ای ایجاب می کند که تا زمانی که هیچ نیروی خارجی به آن وارد نشود، این جهت را حفظ کند. [58] : 59 سه ژیروسکوپ متعامد یک چارچوب مرجع اینرسی ایجاد میکنند و شتابدهندهها شتاب را نسبت به آن قاب اندازهگیری میکنند. سپس از شتاب ها به همراه ساعت می توان برای محاسبه تغییر موقعیت استفاده کرد. بنابراین، ناوبری اینرسی شکلی از محاسبه مرده است که نیازی به ورودی خارجی ندارد و بنابراین نمی تواند توسط هیچ منبع سیگنال خارجی یا داخلی مسدود شود. [59]
قطب نما ژیروسکوپی که برای ناوبری کشتی های دریایی استفاده می شود، شمال هندسی را پیدا می کند. این کار را نه با سنجش میدان مغناطیسی زمین، بلکه با استفاده از فضای اینرسی به عنوان مرجع آن انجام می دهد. پوشش بیرونی دستگاه ژیروقطب نما به گونه ای نگه داشته می شود که با خط شاقول محلی در یک راستا باقی بماند. هنگامی که چرخ ژیروسکوپ داخل دستگاه ژیروسکوپ به سمت بالا می چرخد، نحوه معلق بودن چرخ ژیروسکوپ باعث می شود که چرخ ژیروسکوپ به تدریج محور چرخش خود را با محور زمین هماهنگ کند. تراز با محور زمین تنها جهتی است که محور چرخش ژیروسکوپ می تواند نسبت به زمین ثابت باشد و نیازی به تغییر جهت نسبت به فضای اینرسی نباشد. پس از چرخش، یک ژیروسکوپ میتواند در عرض یک ربع به جهت همسویی با محور زمین برسد. [60]
مثالها (قانون اینرسی چیست)
در این بخش نشده است ذکر هیچ منبعی . لطفاً به بهبود این بخش با افزودن نقل قول به منابع معتبر کمک کنید . مطالب بدون منبع ممکن است به چالش کشیده و حذف شوند . ( جولای 2013 ) ( نحوه و زمان حذف این پیام الگو را بیاموزید ) |
مثال ساده
یک موقعیت رایج در زندگی روزمره را در نظر بگیرید. دو ماشین در یک جاده حرکت می کنند که هر دو با سرعت ثابتی حرکت می کنند. شکل 1 را ببینید. در یک لحظه خاص، آنها 200 متر از هم جدا می شوند. ماشین جلویی با سرعت 22 متر بر ثانیه و ماشین عقب با سرعت 30 متر بر ثانیه حرکت می کند. اگر بخواهیم دریابیم که ماشین دوم چقدر طول می کشد تا به ماشین اول برسد، سه “قاب مرجع” واضح وجود دارد که می توانیم انتخاب کنیم. [61]
ابتدا میتوانستیم دو خودرو را از کنار جاده مشاهده کنیم. ما “قاب مرجع” S خود را به صورت زیر تعریف می کنیم. ما در کنار جاده می ایستیم و دقیقاً در لحظه ای که ماشین دوم از کنار ما می گذرد، ساعت توقف را شروع می کنیم، که اتفاقاً زمانی است که فاصله آنها d = 200 متر است . از آنجایی که هیچکدام از خودروها شتاب نمی گیرند، می توانیم موقعیت آنها را با فرمول های زیر تعیین کنیم ایکس 1 ( تی ) موقعیت بر حسب متر ماشین یک پس از زمان t در ثانیه و ایکس 2 ( تی ) موقعیت ماشین دو بعد از زمان t است .
- ایکس 1 ( تی ) = د + v 1 تی = 200 + 22 تی ، ایکس 2 ( تی ) = v 2 تی = 30 تی .
توجه داشته باشید که این فرمولها همانطور که انتظار میرود، در t = 0 پیشبینی میکنند که ماشین اول 200 متر پایینتر از جاده باشد و ماشین دوم درست در کنار ما باشد، همانطور که انتظار میرود. ما می خواهیم زمانی را پیدا کنیم که در آن ایکس 1 = ایکس 2 . بنابراین، ما تنظیم کردیم ایکس 1 = ایکس 2 و حل کنید برای تی ، به این معنا که:
- 200 + 22 تی = 30 تی ،
- 8 تی = 200 ،
- تی = 25 س ه ج o n د س .
از طرف دیگر، میتوانیم چارچوب مرجع S’ را که در اولین خودرو قرار دارد انتخاب کنیم. در این حالت، اتومبیل اول ساکن است و اتومبیل دوم از پشت با سرعت v 2 − v 1 = 8 m / s نزدیک می شود . به منظور رسیدن به ماشین اول، زمان می برد d / v 2 – v 1 = 200/8 ثانیه . قبل ، یعنی 25 ثانیه، مانند توجه داشته باشید که با انتخاب یک چارچوب مرجع مناسب چقدر مشکل آسان تر می شود. سومین چارچوب مرجع ممکن به ماشین دوم متصل می شود. این مثال شبیه موردی است که قبلاً در مورد آن صحبت شد، به جز اینکه ماشین دوم ساکن است و ماشین اول با سرعت 8 متر بر ثانیه به سمت عقب حرکت می کند .
امکان انتخاب یک چارچوب مرجع چرخان و شتابدهنده وجود داشت که به شیوهای پیچیده حرکت میکرد، اما این امر به پیچیدهتر کردن غیرضروری مشکل کمک میکرد. همچنین لازم به ذکر است که فرد می تواند اندازه گیری های انجام شده در یک سیستم مختصات را به دیگری تبدیل کند. به عنوان مثال، فرض کنید ساعت شما در مقایسه با زمان استاندارد محلی، پنج دقیقه سریع کار می کند. اگر میدانید که اینطور است، وقتی کسی از شما میپرسد ساعت چند است، میتوانید پنج دقیقه از زمان نمایش داده شده در ساعت خود کم کنید تا زمان صحیح را بدست آورید. بنابراین، اندازهگیریهایی که یک ناظر در مورد یک سیستم انجام میدهد به چارچوب مرجع ناظر بستگی دارد (شاید بگویید اتوبوس در ساعت سه و 5 رسیده است، در حالی که در واقع ساعت سه رسیده است).
مثال اضافی (قانون اینرسی چیست)
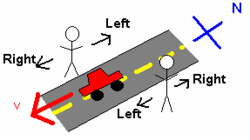
برای مثال ساده ای که فقط جهت گیری دو ناظر را شامل می شود، دو نفر را در نظر بگیرید که در دو طرف خیابان شمالی-جنوبی ایستاده اند. شکل 2 را ببینید. ماشینی از کنار آنها در حال حرکت به سمت جنوب می گذرد. برای شخصی که رو به شرق بود، ماشین به سمت راست حرکت می کرد. با این حال، برای شخصی که رو به غرب بود، ماشین به سمت چپ حرکت می کرد. این اختلاف به این دلیل است که این دو نفر از دو چارچوب مرجع متفاوت برای بررسی این سیستم استفاده کردند.
برای مثال پیچیدهتری که شامل ناظران در حرکت نسبی است، آلفرد را در نظر بگیرید، که در کنار جاده ایستاده و ماشینی را که از چپ به راست از کنار او میگذرد، تماشا میکند. آلفرد در چارچوب مرجع خود نقطه ای را که در آن ایستاده است به عنوان مبدأ، جاده را به عنوان محور x و جهت مقابل خود را به عنوان محور y مثبت تعریف می کند . برای او، ماشین در امتداد محور x با مقداری سرعت v در جهت مثبت x حرکت می کند . چارچوب مرجع آلفرد یک چارچوب مرجع اینرسی در نظر گرفته می شود زیرا او شتاب نمی گیرد (اثراتی مانند چرخش زمین و گرانش را نادیده می گیرد).
حالا بتسی را در نظر بگیرید، شخصی که ماشین را رانندگی می کند. بتسی، در انتخاب چارچوب مرجع خود، مکان خود را به عنوان مبدا، جهت به سمت راست خود را به عنوان محور x مثبت و جهت مقابل خود را به عنوان محور y مثبت تعریف می کند . در این چارچوب، این بتسی است که ساکن است و جهان اطراف او در حال حرکت است – برای مثال، وقتی از کنار آلفرد می گذرد، او را مشاهده می کند که با سرعت v در جهت منفی y حرکت می کند . اگر او به سمت شمال رانندگی می کند، شمال جهت مثبت y است . اگر او به سمت شرق بچرخد، شرق به جهت مثبت y تبدیل می شود .
در نهایت، به عنوان نمونه ای از ناظران غیر اینرسی، فرض کنید کندیس در حال شتاب دادن به ماشین خود است. هنگامی که از کنار او می گذرد، آلفرد شتاب او را اندازه می گیرد و آن را در جهت منفی x می یابد . با فرض ثابت بودن شتاب کندیس، بتسی چه شتابی را اندازه گیری می کند؟ اگر سرعت بتسی v ثابت باشد، او در یک چارچوب مرجع اینرسی قرار دارد، و شتاب را در چارچوب مرجع خود، a در منفی y جهت ، با شتاب آلفرد خواهد یافت. با این حال، اگر او با نرخ A در جهت منفی y می یابد a’ = a − A شتاب می گیرد (به عبارت دیگر، شتاب کندس را کاهش می دهد)، شتاب کندیس را در جهت منفی y – مقداری کوچکتر از آلفرد. اندازه گیری شده. به طور مشابه، اگر او با نرخ A در جهت مثبت y شتاب می گیرد (شتاب می شود)، شتاب کندیس را به صورت a’ = a + A در جهت منفی y – مقداری بزرگتر از اندازه گیری آلفرد مشاهده می کند.

 ، به دیگری، س ”
، به دیگری، س ”  با جمع یا تفریق ساده مختصات:
با جمع یا تفریق ساده مختصات:

 . قاب S’ دارای چرخش دلخواه اما ثابت نسبت به فریم S است . هستند هر دو قاب اینرسی به شرط آنکه جسمی که تحت تأثیر نیرو قرار نگیرد در یک خط مستقیم حرکت می کند. اگر آن حرکت در یک فریم دیده شود، در فریم دیگر نیز به همین شکل ظاهر می شود.
. قاب S’ دارای چرخش دلخواه اما ثابت نسبت به فریم S است . هستند هر دو قاب اینرسی به شرط آنکه جسمی که تحت تأثیر نیرو قرار نگیرد در یک خط مستقیم حرکت می کند. اگر آن حرکت در یک فریم دیده شود، در فریم دیگر نیز به همین شکل ظاهر می شود.









 ( نیروی اویلر )
( نیروی اویلر ) ( نیروی کوریولیس )،
( نیروی کوریولیس )، ( نیروی گریز از مرکز ).
( نیروی گریز از مرکز ).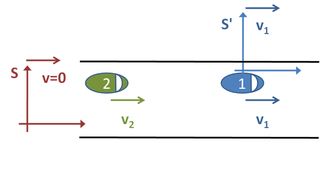
 موقعیت بر حسب متر ماشین یک پس از زمان t در ثانیه و ایکس 2 ( تی )
موقعیت بر حسب متر ماشین یک پس از زمان t در ثانیه و ایکس 2 ( تی )  موقعیت ماشین دو بعد از زمان t است .
موقعیت ماشین دو بعد از زمان t است .
 . بنابراین، ما تنظیم کردیم ایکس 1 = ایکس 2
. بنابراین، ما تنظیم کردیم ایکس 1 = ایکس 2  ، به این معنا که:
، به این معنا که: